CONGRUENZA E ISOMETRIA
Per sovrapporre due figure gli spostamenti compiuti devono essere tali da lasciare inalterata la forma e l’estensione delle figure stesse. Questi spostamenti sono detti movimenti rigidi.
I movimenti rigidi possono essere compiuti sia rimanendo nel piano sia uscendo dal piano su cui giacciono le figure.
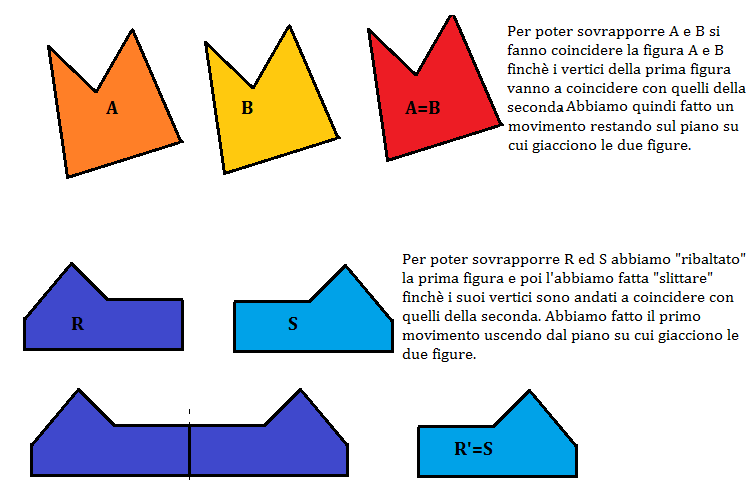
Possiamo allora considerare due diversi tipi di movimento, ovvero di trasformazioni geometriche:
- I movimenti compiuti nel piano in cui giacciono le figure da sovrapporre sono detti movimenti diretti, essi danno origine a figure direttamente congruenti.
- I movimenti compiuti uscendo dal piano in cui giacciono le figure da sovrapporre sono detti movimenti inversi; essi danno origine a figure inversamente congruenti.
Le trasformazioni geometriche che non deformano le figure, ma ne cambiano solo la posizione, determinano figure direttamente o inversamente congruenti, sono dette trasformazioni isometriche o isometrie.
Sono isometrie la traslazione, la rotazione e le simmetrie (centrale ed assiale) che trasformano una figura data in un’altra ad essa direttamente o inversamente congruente, mantenendo inalterata la lunghezza dei segmenti e l’ampiezza degli angoli delle figure.