La similitudine è una trasformazione non isometrica che trasforma una figura nella sua immagine.
Quindi due figure che hanno la stessa forma senza necessariamente avere la stessa estensione, cioè senza essere equivalenti, sono dette simili.

Di una stessa figura possiamo avere due riproduzioni, una più grande e l’altra più piccola adoperando scale di riduzione diverse.
E se riflettiamo vediamo che tutte le dimensioni delle due figure mutano in modo proporzionale, mentre tutti gli angoli si conservano uguali, per cui se un angolo muta, la figura cambia di forma.
Vediamo quando possiamo affermare che due poligoni sono simili. Disegniamo un poligono ABCD ed un poligono A’B’C’D’ ingrandito il doppio rispetto al primo poligono; esso avrà gli angoli ordinatamente uguali a quelli del poligono dato e i lati uguali al doppio dei corrispondenti lati di tale poligono.
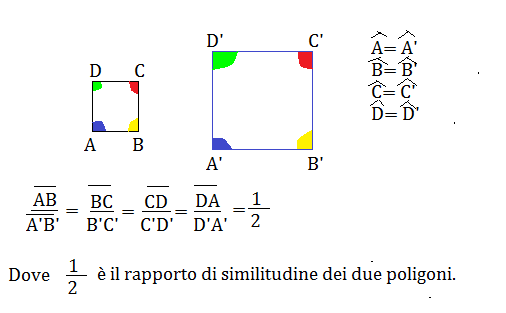
Diciamo perciò che:
due poligoni sono simili se hanno gli angoli corrispondenti uguali ed i lati corrispondenti proporzionali e quindi il rapporto tra essi è costante.
L’ampiezza degli angoli e il rapporto fra i lati corrispondenti sono invarianti per la similitudine. Il rapporto fra due lati corrispondenti prende il nome di rapporto di similitudine e si indica con K.
Si può verificare che:
- se k>1 F’ è un ingrandimento di F;
- se k=1 F’ ed F sono congruenti;
- se k<1 F’ è una riduzione di F.