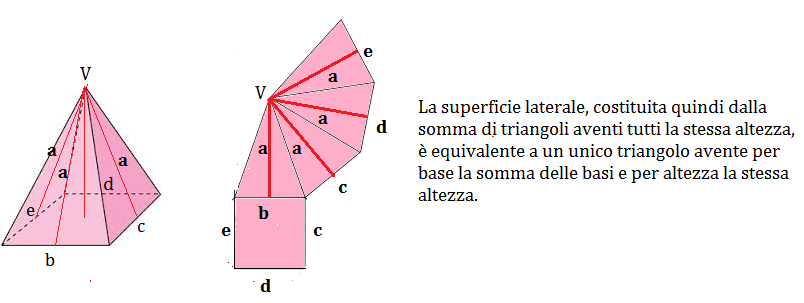
Prendiamo il modello di una piramide retta avente per base un quadrilatero, costruito con un cartoncino. Tagliamolo lungo uno spigolo laterale e lungo tutti gli spigoli di base, eccetto uno e stendiamolo su un piano.
Otteniamo così lo sviluppo della superficie totale della piramide. Tale sviluppo è costituito dal poligono di base della piramide e da una figura piana costituita da tanti triangoli quanti sono i triangoli della superficie laterale della piramide aventi tutti per altezza l’apotema della piramide. Questa figura piana è lo sviluppo della superficie laterale della piramide. Osservando questo sviluppo e indicando la misura della lunghezza dei quattro spigoli di base rispettivamente con b, c, d, e e con a la misura dell’apotema della piramide.
Indicando con l’area della superficie laterale, con 2p il perimetro di base e con a l’apotema avremo:
da cui si possono ricavare le formule inverse che ci permettono di calcolare:
- l’apotema conoscendo l’area della superficie laterale e il perimetro di base :
- il perimetro di base conoscendo l’area della superficie laterale e l’apotema :
L’area della superficie laterale di una piramide retta si ottiene moltiplicando il perimetro di base per la misura dell’apotema e dividendo per due il perimetro ottenuto.
L’area della superficie totale si otterrà addizionando all’area della superficie laterale l’area di base quindi:
da cui
e
L’area della superficie totale di una piramide retta si ottiene addizionando all’area della superficie laterale l’area del poligono di base.