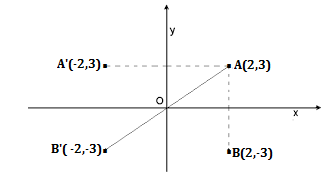
Due punti si dicono simmetrici rispetto ad una retta se hanno uguale distanza dalla retta.
Osserviamo la figura :
- A (2, 3) e A’ (-2, 3) hanno ascisse opposte e ordinate uguali: sono simmetrici rispetto all’asse y.
- A (2, 3) e B’ (-2,-3) hanno ascisse e ordinate opposte: sono simmetrici rispetto all’origine O degli assi.
- A (2, 3) e B (2, -3) hanno ascissa uguale e ordinate opposte: sono simmetrici rispetto all’asse x.
Esercizio n° 1
Rappresenta in un piano cartesiano i simmetrici del segmento avente per estremi A(-5 ; -6) e B(-1; -2).
Esercizio n° 2
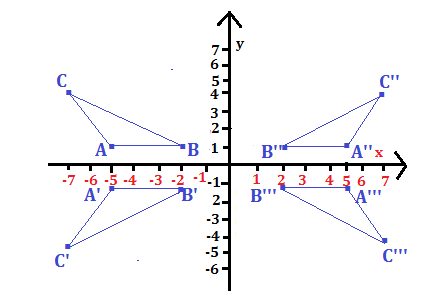
Costruisci i simmetrici del triangolo di vertici A (-5; +1), B(-2; +1), C(-7; +4)
I triangoli hanno per vertici i simmetrici dei vertici A,B e C, quindi:
a il triangolo A’B’C’ è il simmetrico rispetto all’asse x e i suoi vertici sono:
A’ (-5; -1), B’ (-2; -1) e C’ (-7; -4)
b il triangolo A”B”C” è il simmetrico rispetto all’asse y e i suoi vertici sono:
A”(+5; +1), B” (+2; +1) e C”(+7; +4)
c il triangolo A”’B”’C”’ è il simmetrico rispetto all’origine e i suoi vertici sono:
A”’ (+5; -1), B”'(+2; -1) e C”'(+7; -4)
Quindi non è difficile individuare tali punti , basta essere precisi e stare attenti ai numeri che si considerano.