Nel caso dell’equazione :
y=mx+q in cui m e q sono numeri qualsiasi, ed m è il coefficiente angolare della retta.
Se vogliamo trovare il punto d’intersezione della retta con l’asse delle y, poichè la sua equazione è x=0, andando a sostituire lo zero nell’equazione generale avremo che y=o·x+q quindi y=q.
Vediamo che il numero q rappresenta l’ordinata del punto in cui la retta taglia l’asse y.
Se vogliamo trovare il punto d’intersezione della retta con l’asse delle x, poichè la sua equazione è y=0, andando a sostituite lo zero alla y avremo: o=mx+q ⇒mx=-q ⇒ x=-q\m.
Vediamo che il numero -q\m rappresenta l’ascissa del punto in cui la retta taglia l’asse x.
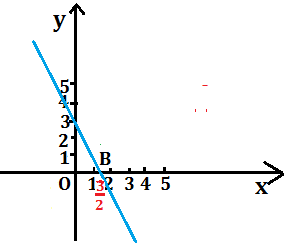
Consideriamo la retta di equazione y=-2x+3
Per trovare il punto l’intersezione con l’asse y consideriamo che la sua equazione è x=0 quindi avremo :
y=3, tale punto avrà come coordinate (0,+3).
Per trovare il punto d’intersezione con l’asse x consideriamo che la sua equazione è y=0 quindi avremo:
-2x+3=0 ⇒ x=3\2.
Concludiamo perciò che la retta interseca gli assi nei punti A(0,3) e B(3\2; 0).