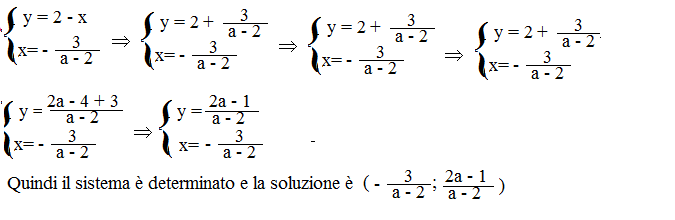I sistemi letterali sono quei sistemi che presentano almeno una equazione letterale, cioè oltre alle normali incognite, presentano anche lettere detti parametri che rappresentano dei numeri.
Questi sistemi si risolvono con i normali metodi usati per i sistemi letterali normali, ma bisogna escludere per i parametri i valori eventuali che fanno perdere significato alle equazioni del sistema, cioè bisogna fare la condizione di esistenza. Inoltre, bisogna stabilire , con una discussione , per quali valori il sistema risulta determinato, indeterminato o impossibile.
Per capire meglio consideriamo degli esempi:
A questo punto poichè il determinante dipende dal parametro a, bisogna fare una discussione.
Se D= 0 significa che -2a +1 =0 ⇒ 2a =1 quindi a = 1\2 quindi
=2a²-a = 2 ·1\4 – 1\2= 0
= a – 2a² = 1\2 – 2 ·1\4= 0
Quindi il sistema sarà indeterminato.
Se D≠0 significa che -2a +1 ≠0 ⇒ 2a ≠ 1 quindi a ≠ 1\2 e il sistema è determinato.
La soluzione del sistema è (-a; a)
Vediamo ora un altro esempio:
Se a – 2 = 0, cioè se a = 2 otteniamo 0x = -3 e quindi il sistema è impossibile.
Se a – 2 ≠0, cioè se a ≠ 2, possiamo dividere la seconda equazione per a – 2 e otteniamo: