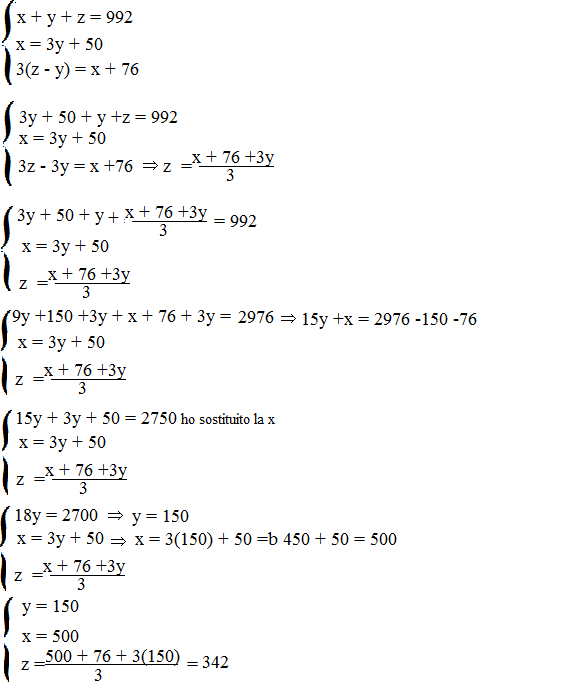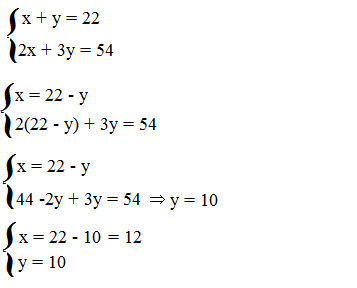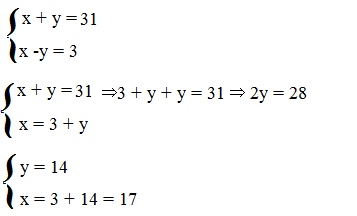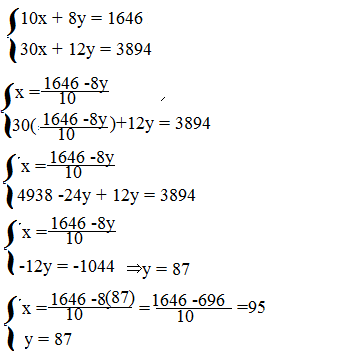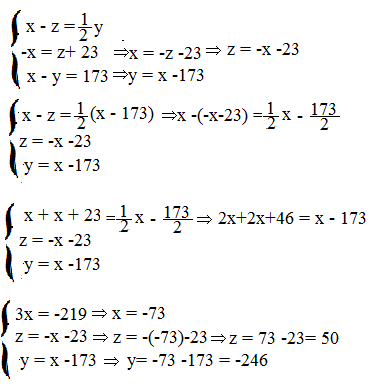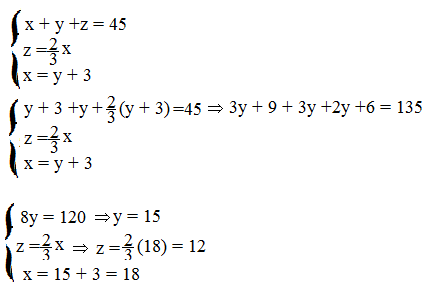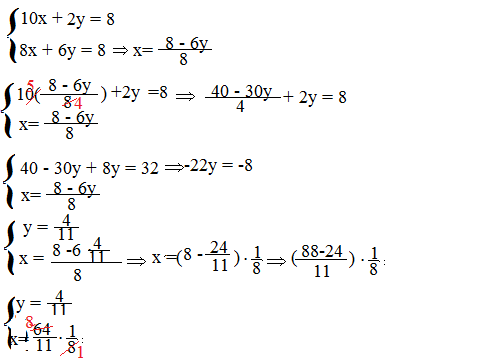Problemi che si risolvono con i sistemi di equazioni.
Problema n° 1
La somma di tre numeri è 87. Sapendo che sono consecutivi trova i tre numeri.
Problema n° 2
La somma di tre numeri è 192. Sapendo che il primo supera di 10 il quintuplo del secondo e che il terzo è 1\15 del secondo, trova i tre numeri.
Problema n° 3
La somma di tre numeri è 992. Sapendo che il primo supera di 50 il triplo del secondo e che il triplo della differenza tra il terzo e il secondo supera di 76 il primo, trova i tre numeri.
Problema n° 4
Una scatola contiene forchette a 2 e a 3 punte. Sapendo che le forchette in totale sono 22 e che le punte in totale sono 54 calcola quante sono le forchette a 2 punte e quante quelle a tre punte.
Problema n° 5
Lucia e Elena sono sorelle. La somma della loro età è 31 e Lucia è nata tre anni prima di Elena. Quanti anni ha ciascuna.
Problema n° 6
10 sacchi di frumento e 8 di mais pesano 1646 kg; 30 sacchi di frumento e 12 di mais, rispettivamente uguali ai precedenti, pesano 3894 kg. Quanto pesa ciascun sacco di frumento e ciascun sacco di mais.
Problema n° 7
Trova tre numeri tali che la differenza tra il primo e il terzo sia la metà del secondo, inoltre l’opposto del primo superi di 23 il terzo numero e il primo differisca dal secondo di 173.
Problema n° 8
La somma delle età di Paolo , Marco e Gino è 45. Sapendo che Gino ha 2\3 degli anni di Paolo , e che Paolo ha 3 anni in più di Marco, determina le loro età.
Problema n° 9
Due segmenti AB e CD sono tali che la somma di 10 segmenti congruenti ad AB con due segmenti congruenti a CD è 8 dm. Inoltre la somma di 8 segmenti congruenti ad AB con 6 segmenti congruenti a CD è 8 dm. Determina la lunghezza di AB e di CD.
SVOLGIMENTO
Problema n° 1
La somma di tre numeri è 87. Sapendo che sono consecutivi trova i tre numeri.
DATI
x = 1° numero
x+1 = 2°numero
x+2 = 3° numero
Equazione: x +(x+1)+( x+2) = 87
3x + 3 = 87 ⇒ 3x= 84 ⇒ x = 84\3 = 28
Problema n° 2
La somma di tre numeri è 192. Sapendo che il primo supera di 10 il quintuplo del secondo e che il terzo è 1\15 del secondo, trova i tre numeri.
DATI
x = 1° numero
y= 2° numero
z = 3° numero
SVOLGIMENTO
la somma dei tre numeri è 192→ x + y + z = 192
Il primo supera di 10 il quintuplo del secondo → x – 5y = 10
Il terzo è 1\15 del secondo → z = 1\15 y
I numeri cercati sono 160, 30 e 2
Problema n° 3
La somma di tre numeri è 992. Sapendo che il primo supera di 50 il triplo del secondo e che il triplo della differenza tra il terzo e il secondo supera di 76 il primo, trova i tre numeri.
DATI
x = 1° numero
y= 2° numero
z= 3° numero
SVOLGIMENTO
La somma dei tre numeri è 192 → x +y +z = 192
il primo supera di 50 il triplo del secondo → x = 3y + 50
il triplo della differenza tra il terzo e il secondo supera 76 il primo →3(z – y)= z+76
I numeri cercati sono 500, 150 e 342
Problema n° 4
Una scatola contiene forchette a 2 e a 3 punte. Sapendo che le forchette in totale sono 22 e che le punte in totale sono 54 calcola quante sono le forchette a 2 punte e quante quelle a tre punte.
DATI
x = forchette a 2 punte
y = forchette a 3 punte
SVOLGIMENTO
le forchette in totale sono 22 → x + y = 22
le punte in totale sono 54→ 2x + 3y = 54
Le forchette a 2 punte sono 12 e quelle a 3 punte sono 10
Problema n° 5
Lucia e Elena sono sorelle. La somma della loro età è 31 e Lucia è nata tre anni prima di Elena. Quanti anni ha ciascuna.
DATI
x= età di Lucia
y= età di Elena
SVOLGIMENTO
somma dell’età di Lucia e Elena è 31 → x+ y = 31
Lucia è nata tre anni prima di Elena → x – y = 3
L’età di Lucia è 17 e l’età di Elena è 14
Problema n° 6
10 sacchi di frumento e 8 di mais pesano 1646 kg; 30 sacchi di frumento e 12 di mais, rispettivamente uguali ai precedenti, pesano 3894 kg. Quanto pesa ciascun sacco di frumento e ciascun sacco di mais.
DATI
x = frumento
y = mais
SVOLGIMENTO
10 sacchi di frumento e 8 di mais pesano 1646 kg → 10x + 8y = 1646
30 sacchi di frumento e 12 di mais pesano 3894 kg → 30x + 12y = 3894
Un sacco si frumento pesa 95 kg, invece, un sacco di mais pesa 87 kg
Problema n° 7
Trova tre numeri tali che la differenza tra il primo e il terzo sia la metà del secondo, inoltre l’opposto del primo superi di 23 il terzo numero e il primo differisca dal secondo di 173.
DATI
x= 1° numero
y= 2° numero
z= 3° numero
SVOLGIMENTO
la differenza tra il 1° e il 3° è la metà del secondo → x – z= 1\2 y
l’opposto del primo supera di 23 il terzo numero → -x = z + 23
il primo differisce dal secondo di 173 → x – y = 173
I numeri sono -73, -246 e 50
Problema n° 8
La somma delle età di Paolo , Marco e Gino è 45. Sapendo che Gino ha 2\3 degli anni di Paolo , e che Paolo ha 3 anni in più di Marco, determina le loro età.
DATI
x= età di Paolo
y= età di Marco
z= età di Gino
SVOLGIMENTO
la somma dell’età di Paolo, Marco e Gino è 45 → x+y+z= 45
Gino ha 2\3 degli anni di Paolo →z = 2\3x
Paolo ha 3 anni in più di Marco → x = y + 3
Paolo ha 18 anni, Marco 15 anni e Gino 12 anni
Problema n° 9
Due segmenti AB e CD sono tali che la somma di 10 segmenti congruenti ad AB con due segmenti congruenti a CD è 8 dm. Inoltre la somma di 8 segmenti congruenti ad AB con 6 segmenti congruenti a CD è 8 dm. Determina la lunghezza di AB e di CD.
DATI
x = AB
y= CD
SVOLGIMENTO
la somma di 10 segmenti congruenti ad AB con due segmenti congruenti a CD è 8 dm →10x +2y = 8
a somma di 8 segmenti congruenti ad AB con 6 segmenti congruenti a CD è 8 dm→ 8x + 6y = 8