ESERCIZIO N° 1
In ciascuno dei seguenti casi, scrivi l’equazione della retta passante per i punti A e B.
a)A(0; -1) B(5; 3)
b)A(0; 0) B(4; -2)
c)A(- 1; 1\5) B(1\3; 2)
d)A(1\4; 1\2) B(1; -2)
ESERCIZIO N° 2
In ciascuno dei seguenti casi, scrivi l’equazione dell’asse del segmento che per estremi i punti A e B.
a)A(-1; 4) B(2; -3)
b)A(2; -5) B(2; 3)
c)A(-1; -3) B(0; 4)
SVOLGIMENTO
ESERCIZIO N° 1
In ciascuno dei seguenti casi, scrivi l’equazione della retta passante per i punti A e B.
a)A(0; -1) B(5; 3)
L’equazione della retta passante per due punti è :
quindi andando a sostituire le coordinate dei punti avremo:
⇒ 5y + 5= 4x ⇒ 4x -5y – 5=0
b)A(6; 5) B(6; 11)
quindi y=5
c)A(- 1; 1\5) B(1\3; 2)
quindi
20y-4=27x+27 ⇒ 20y -27x -31=0
d)A(1\4; 1\2) B(1; -2)
quindi
6y+30x -8=0 semplificando otteniamo 3y+15x-4=0
ESERCIZIO N° 2
In ciascuno dei seguenti casi, scrivi l’equazione dell’asse del segmento che per estremi i punti A e B.
Prima di partire con l’esercizio dobbiamo ricordare che l’asse di un segmento è la retta a esso perpendicolare e passante per il suo punto medio.
a)A(-1; 4) B(2; -3)
Scriviamo l’equazione della retta passante per due punti.
⇒
Una generica retta perpendicolare a tale retta passante per A e B quindi dovrà avere coefficiente angolare pari al suo reciproco e cioè m= 3\7
Avremo y = 3\7x + q.
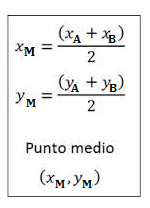
Calcoliamo ora le coordinate del punto medio di AB a avremo:
Le coordinate dl pu8nto medio saranno:
quindi
a questo punto poichè sappiamo che la retta y = 3\7x + q. passa per il punto medio allora andiamo a sostituire le coordinate di M nella retta e otteniamo:
L’asse cercato avrà quindi equazione:
b)A(2; -5) B(2; 3)
Scriviamo l’equazione della retta passante per due punti.
sostituiamo le coordinate
y = -5 e il suo coefficiente angolare è 0.
Il punto medio è:
⇒ M(2; -1)
La retta y = mx + q in questo caso poichè m=0 è y=q, visto che passa per il punto medio andiamo a sostituire le sue coordinate e avremo:
-1 = q quindi q= -1 di conseguenza y=-1
c)A(-1; -3) B(0; 4)
Scriviamo l’equazione della retta passante per due punti.
quindi y + 3 = 7x + 7 ⇒ y = 7x + 4 la sua m=7
Il punto medio del segmento AB è:
La retta generica è y= mx + q il coefficiente angolare che andrò a sostituire, visto che l’asse è perpendicolare sarà il reciproco quindi m= – 1\7
La retta sarà y = – 1\7x + q , poichè passa per il punto medio sostituisco le coordinate del punto e ottengo:
L’asse cercato è: