Tra due insiemi A e B è stabilita una corrispondenza quando è fissata una regola che associa elementi di A a elementi di B.
Una relazione di questo tipo è chiamata funzione.
Una corrispondenza tra due insiemi A e B si dice univoca se associa a ogni elemento di A un solo elemento di B.
Una corrispondenza tra due insiemi A e B si dice biunivoca se associa a ogni elemento di A un solo elemento di B e viceversa, a ogni elemento di B associa un solo elemento di A.
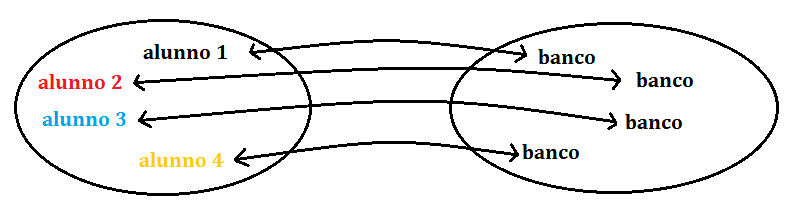
Consideriamo l’insieme A degli alunni di una classe e l’insieme B dei banchi di un’aula. Se ogni alunno occupa un banco e nell’aula non rimangono banchi vuoti vediamo che possiamo far corrispondere ad ogni alunno un banco, e viceversa, ad ogni banco un alunno.
In tal modo ad ogni elemento di A viene associato un solo elemento di B e, viceversa, ad ogni elemento di B viene associato un solo elemento di A. Quindi c’è una corrispondenza biunivoca.
Se tra due insiemi A e B possiamo stabilire una corrispondenza biunivoca, essi hanno lo stesso numero di elementi, cioè sono equipotenti. In simboli si scriverà A≡B che si legge A è equipotente a B.