DI COSA SI OCCUPA LA FISICA?
La fisica studia i fenomeni naturali, come la luce l’energia contenuta nella materia e si propone di trovare delle leggi, espresse mediante formule matematiche, che li descrivano.
Essa inoltre parla di grandezze, cioè di quantità che possono essere misurate con degli strumenti.
La fisica a seconda del campo di studio si divide in:
- meccanica che studia l’equilibrio e il movimento dei corpi. Quindi essa si occupa di descrivere il movimento dei pianeti e la caduta degli oggetti sulla Terra. Le leggi della meccanica servono sia per mettere un orbita un satellite ma anche per costruire una macchina e tantissimo altro.
- termodinamica che studia i fenomeni legati al calore e alla temperatura. Sulle leggi della termodinamica i basano tutte le macchine che trasformano il calore in movimento come il motore a scoppio.
- acustica che studia le proprietà del suono quindi serve per progettare strumenti musicali le casse di un impianto hi-fi.
- ottica che si occupa delle proprietà della luce e le sue leggi consentono di progettare occhiali, macchine fotografiche, telescopi ed altro.
- elettromagnetismo che studia i fenomeni elettrici e magnetici e le sue leggi descrivono il funzionamento dei circuiti e dei motori elettrici, su di essa si basano le telecomunicazioni e molto altro.
- fisica quantistica che studia i corpi molto piccoli come atomi, elettroni e nuclei e comprende la fisica atomica e nucleare. Utile per la costruzione di laser, transistor, centrali nucleari ecc.
- astrofisica e cosmologia studiano i corpi celesti e serve per progettare reattori a fusione nucleare.
Quindi tutto ciò che facciamo e osserviamo ha a che fare con la fisica. Quando facciamo bollire l’acqua, un qualcosa per noi normale, stiamo usando in modo intuitivo una legge della termodinamica secondo la quale l’acqua a pressione atmosferica e a livello del mare, bolle a 100°C. Ma anche tutte le tecnologie che ci circondano nella quotidianità hanno a che fare con le leggi della fisica.
LE GRANDEZZE FISICHE
Una grandezza fisica è una quantità, cioè una proprietà di un corpo o di un fenomeno che può essere misurata con strumenti di misura come l’altezza di un muro, la temperatura dell’acqua, la velocità di un’auto ecc.
Per misurare una grandezza occorre prima di tutto l’ unità di misura che è una quantità della stessa specie di quella presa in esame, il cui valore è stabilito pari a 1.
Quindi misurare una grandezza significa stabilire quante volte l’unità di misura è contenuta in tale grandezza.
Per esempio per misurare la lunghezza di un tavolo potremmo usare delle forchette e dire quante volte è contenuta una forchetta. Però per far sì che ci posa essere comunicazione con gli altri è bene sempre usare una unità di misura universale che è il metro.
Per comunicare il risultato di una misura bisogna scrivere il numero seguito dall’unità di misura, per esempio la velocità di una macchina:
v= 120 km\h dove i chilometri all’ora è l’unità di misura
SISTEMA INTERNAZIONALE DI UNITA’
Affinché una misura abbia senso deve essere espressa attraverso un numero e un’unità di misura.
La comunità scientifica internazionale ha identificato sette grandezze indipendenti, le grandezze fondamentali (Tabella 1), dalle quali possono essere ricavate tutte le altre, grandezze derivate.(Tabella 2).
Il sistema metrico fondato sulle sette grandezze fondamentali è chiamato Sistema Internazionale di misura (SI). Esso è stato fondato nel 1960.
Aderendo a un comune sistema di unità di misura, gli scienziati di tutto il mondo possono interpretare facilmente i risultati di ognuno.
Tabella 1. Le grandezze fondamentali e le loro unità di misura
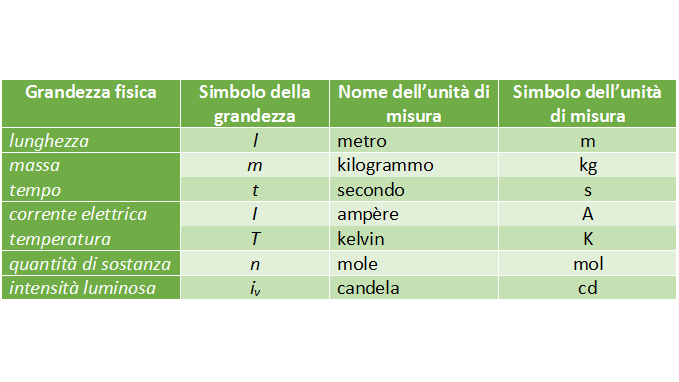
Dalla combinazione algebrica (moltiplicazioni e divisioni) delle sette unità fondamentali si possono ottenere le unità di misura delle grandezze derivate.
Tabella 2. Alcune grandezze derivate

Non sempre le unità di misura fondamentali per una data quantità sono convenienti da utilizzare.
Spesso, per evitare l’uso di numeri troppo grandi o troppo piccoli è comodo esprimere i valori delle misure con multipli o sottomultipli.
Ad esempio, il tempo impiegato da un computer per leggere e scrivere dei dati è dell’ordine dei millesimi di secondo: un possibile valore è 0,009 s che può essere scritto in modo sintetico utilizzando dei prefissi che indicano il multiplo o il sottomultiplo di una determinata grandezza.
Un prefisso indica quante volte un’unità di misura deve essere moltiplicata o divisa per 10 per ottenere in numero desiderato.
In tabella 3 sono mostrati i principali prefissi delle unità di misura.
Se utilizziamo il prefisso milli- (m), possiamo scrivere 0,009 secondi come 9 millisecondi, o 9 ms:
9 ms = 9\1000 s = 0,009 s
Notiamo che dividere per 1000 equivale a moltiplicare per 0,001.
Tabella 3. Principali prefissi delle unità di misura
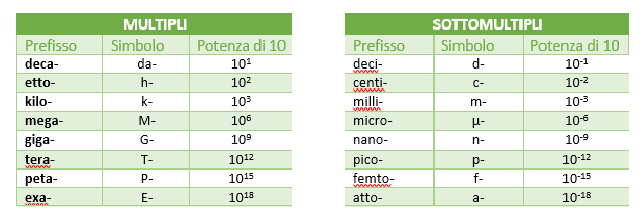
Per scrivere i valori delle misure occorre rispettare delle semplici regole. I simboli delle unità di misura:
- devono sempre sempre seguire il valore numerico quindi scriveremo 25 cm e non cm 25;
- vanno scritti con l’iniziale minuscola, fanno eccezione M e G e i nomi di unità che derivano da nomi propri come W , unità di misura della potenza, che sta per watt appunto da James Watt. Però le parole che indica l’unità di misura si scrivono in minuscolo.
LA NOTAZIONE SCIENTIFICA
Poichè i fisici lavorano con numeri molto grandi o numeri molto piccoli, invece di scrivere tutti gli zeri in questi numeri, si sono inventati la notazione scientifica, cioè si scrivono come potenza di dieci.
La notazione scientifica è un modo per esprimere un valore come prodotto di un numero compreso tra 1 e 10 e una potenza di 10. Cioè lo troveremo nella forma A • , dove A è quel numero compreso tra 1 e 10, invece n è un numero intero positivo o negativo.
Nello scrivere il numero in forma esponenziale si scriverà il primo numero partendo da sinistra verso destra che sia diverso da zero e si pone la virgola: il valore di n quindi dipenderà dal numero di posti che ha attraversato la virgola, se essa si è spostata verso sinistra l’esponente è positivo, verso destra è negativo.
Per esempio se dobbiamo scrivere 300 000 000 secondo la notazione scientifica sarà 3,0 • . Dove l’esponente 8 significa che se volessimo riscrivere il numero per intero al 3 dovremmo aggiungere 8 zeri.
Ovviamente per numeri più piccoli di 1 si usa l’esponente negativo. Per esempio se dovessimo scrivere 0,00097, con la notazione scientifica diventerà 9,7 • .
Quindi la notazione scientifica è vantaggiosa perchè ci permette di scrivere un numero in modo compatto.
Quando un numero è critto in notazione scientifica le cifre significative sono quelle del coefficiente.
Se ci troviamo a dover moltiplicare dei numeri scritti secondo la notazione scientifica; moltiplicheremo prima i numeri che compaiono prima del 10 e poi riscrivere il 10 il cui esponente sarà la somma degli esponenti dei fattori.
Quindi per eseguire moltiplicazioni e divisioni con numeri scritti secondo la notazione scientifica lo si fa utilizzando le proprietà delle potenze.
Per esempio ( 6,0 • ) ( 5,0 •
) = 30 •
ma la scrittura giusta sarà 3,0 •
Se ci troviamo invece a dover affrontare una divisione tra numeri scritti secondo la notazione scientifica, si devono dividere i numeri che compaiono prima del 10 e poi si devono sottrarre gli esponenti.
Per esempio (9,0 • ) : (3,0 •
)= 3,0 •
ORDINE DI GRANDEZZA
L’ordine di grandezza di un numero è la potenza di 10 che più si avvicina a quel numero, cioè che meglio approssima il valore della misura.
Ovviamente se il numero è espresso secondo la notazione scientifica, valutare l’ordine di grandezza è immediato. Se il coefficiente del numero in notazione scientifica è maggiore o uguale a 5 si arrotonda il coefficiente a 10 e si moltiplica il coefficiente per la potenza già presente; l’ordine di grandezza è dato dalla potenza di 10 ottenuta.
Esempio
Raggio del Sole= 7,0 • m= 10 •
m=
m → ordine di grandezza
Se il coefficiente del numero in notazione scientifica è minore di 5, il coefficiente reta lo stesso e l’ordine di grandezza è quello della potenza di 10
Esempio
Raggio lunare = 1,7 • m= 2 •
m→ ordine di grandezza
APPROSSIMAZIONE DI UN NUMERO
Approssimare una misura significa seguire delle semplici regole:
- se la cifra da approssimare è maggiore o uguale a 5 si aumenta di 1 la cifra precedente (approssimazione per eccesso). Per esempio 8,357 se dovessimo approssimare ai centesimi diventerebbe 8,36
- se la prima cifra da trascurare è minore di 5 la cifra precedente rimarrà la stessa (approssimazione per difetto)
CIFRE SIGNIFICATIVE
Per capire come si scelgono le cifre significative consideriamo una tabella.
| Numero | Cifre significative |
| 0,00342 | 3 |
| 0,0342 | 3 |
| 0,342 | 3 |
| 34,2 | 3 |
| 0,3420 | 4 |
| 34,20 | 4 |
| 3420,0 | 5 |
Le regole per effettuare la scelta delle cifre significative è la seguente:
- tutti i numeri diversi da zero si considerano cifre significative;
- gli zeri che precedono, a sinistra, la prima cifra diversa da zero non sono significativi;
- gli zeri terminali, a destra di una cifra decimale diversa da zero, sono cifre significative;
- il numero di cifre significative non cambia se si cambia l’unità di misura
Se per esempio si eseguono operazioni di misurazione e si ottengono numeri con cifre non tutte significative, il risultato deve essere arrotondato.
LE CIFRE SIGNIFICATIVE NEI CALCOLI
Può capitare di trovarci a calcolare misure indirette e vediamo quali siano le regole da seguire:
- Moltiplicazioni e divisioni di misure. Il risultato deve avere le stesse cifre significative del dato che ne ha meno.
Ad esempio 5,870 m • 2,5 m = 14,675 m²
- L’ultima cifra significativa del risultato si trova in corrispondenza dell’ultima colonna a destra che contiene il risultato di un’operazione tra cifre tutte significative.
L’INTERVALLO DI TEMPO
Nella vita di tutti i giorni quando parliamo di tempo ci riferiamo quasi sempre ad intervalli di tempo tra due eventi precisi come la partenza e l’arrivo. Quindi quando parliamo di tempo ci riferiamo alla durata di un fenomeno.
Proprio la durata di alcuni fenomeni periodici, cioè che si ripetono sempre uguali è usata per definire le unità di misura del tempo.
Per misurare la durata di un fenomeno (intervallo di tempo tra inizio e fine) si conta quante volte la durata di un fenomeno periodico è contenuta nella durata da misurare.
L’unità di misura dell’intervallo di tempo nel S.I. è il secondo (s), definito come l’intervallo di tempo impiegato da una particolare onda elettromagnetica, emessa da atomi di cesio-133 , per compiere 9 192 631 770 oscillazioni.
MULTIPLI E SOTTOMULTIPLI DEL SECONDO
Nome Simbolo Valore in secondi
anno a 3,18 x
giorno d 86400
ora h 3600
minuto min 60
millisecondo ms 1\1000=
microsecondo μs 1\1000000=
LA LUNGHEZZA
In tempi antichi per misurare la lunghezza di qualcosa si usava la spanna cioè la distanza tra la punta del pollice e quella del mignolo con la mano aperta. Ovviamente non era un modo di misurare oggettivo perchè una misura variava di persona in persona.
Oggi l’unità di misura nel sistema internazionale è il metro (m), definito come la distanza percorsa dalla luce, nel vuoto, in un intervallo di tempo pari a 1\299792458 di secondo.
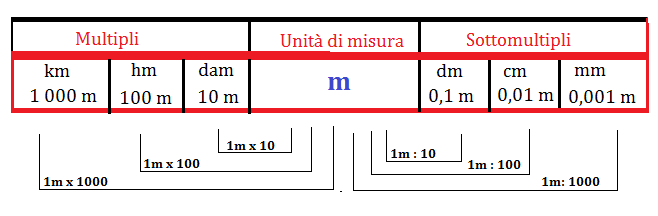
Vediamo quale è la scala per misurare la lunghezza e quindi i multipli e sottomultipli del metro.
Poichè la misura della lunghezza fa parte del sistema metrico decimale, le varie unità di misura secondarie sono multipli e sottomultipli del metro secondo il numero 10.
Quindi: per trasformare una misura di lunghezza da un’unità a un’altra di cui è multipla, si moltiplica per 10, 100, 1 000… cioè se si fanno spostamenti verso destra; per trasformarla in un’altra di cui è sottomultipla si divide per 10, 100, 1000,..cioè se si fanno spostamenti verso sinistra.
ESEMPI
1) 21 cm= 0,21 m; 2) 6,53 dam= 653 dm; 3) 845 dm = 84500 mm;
4) 9,76 m=0,976 dam; 5) 83 Km= 83000 m ;6)71,7 m = 0,717 hm;
7)5,3 mm= 0,0053 m ; 8)0,2 Km = 200 m; 9)0,08 dam = 80 cm;
10) 0,79 hm= 679 m.
Per le equivalenze delle aree per ogni spostamento bisogna moltiplicare o dividere per 100, invece per il volume bisogna moltiplicare o dividere per 1000.
LA MASSA
La massa esprime la quantità di materia e si misura con la bilancia a bracci. Strumento costituito da un’asta rigida che può oscillare intorno al suo punto di mezzo (fulcro). Ai due estremi dell’asta sono agganciati due piatti.
In pratica due corpi hanno la stesa massa se quando sono posti sui due piatti della bilancia, i piatti non salgono nè scendono quindi retano in equilibrio.
L’unità fondamentale della massa è il kilogrammo definito come il peso del campione di platino e iridio, custodito al museo di Sevres a Parigi, e corrisponde anche alla massa di un dm³ di acqua distillata a livello del mare alla temperatura di 4 ° C.
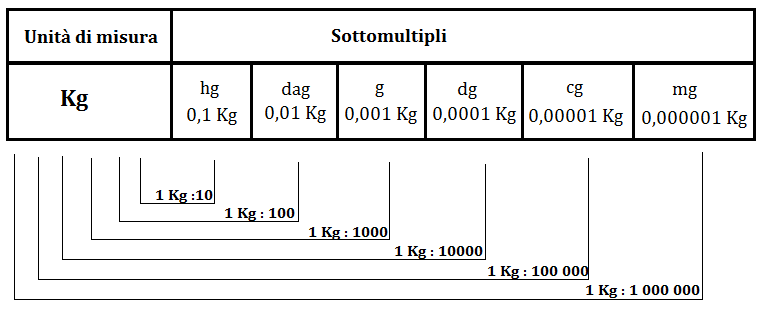
Secondo le ultime direttive europee l’unico multiplo del Kg è il megagrammo (Mg) (ex tonnellata) che equivale a 1000 Kg.
Per trasformare una misura di massa da un’unità in un’altra:
- Se è di ordine superiore, si divide per 10, 100, 1000.
270 g = 2, 70 hg abbiamo diviso per 100 poichè hg è di ordine superiore rispetto a g e quindi ci siamo spostati di due posti verso sinistra;
42 dg = 0,00042 Mg abbiamo diviso per 100 000 poichè Mg è di ordine superiore rispetto a dg e quindi ci siamo spostati di 5 posti verso sinistra.
- Se è di ordine inferiore, si moltiplica per 10, 100, 1 000.
32 Kg = 320000 dg abbiamo moltiplicato per 10 000 poichè dg è di ordine inferiore rispetto a Kg e quindi ci siamo spostati di 4 posti verso destra;
270 hg = 27000 g abbiamo moltiplicato per 100 poichè g è di ordine inferiore rispetto ad hg e quindi ci siamo spostati di due posti verso destra.
LA DENSITA’
La densità è quella grandezza derivata che caratterizza ogni materiale, infatti se per esempio riempiamo due bottiglie identiche una con latte e l’altra con acqua e le mettiamo su una bilancia notiamo che il peso del latte è maggiore dell’acqua a parità di volume occupato quindi vorrà dire che la massa del latte è maggiore di quella dell’acqua e questo avviene perchè hanno diversa densità .
La densità (d ) di un corpo è uguale al rapporto tra la sua massa m e il suo volume V , quindi è direttamente proporzionale alla massa e inversamente proporzionale al volume.
La sua unità di misura è kg \m³
Le sue formule inverse sono:
m= d • V
Se ci troviamo nella situazione di dover fare un’equivalenza dell’unità di misura della densità dobbiamo fare attenzione. Se per esempio abbiamo:
0,36 g\cm³ e lo dobbiamo portare a kg\m³ facciamo in questo modo: