ALTEZZE DI UN TRIANGOLO E ORTOCENTRO

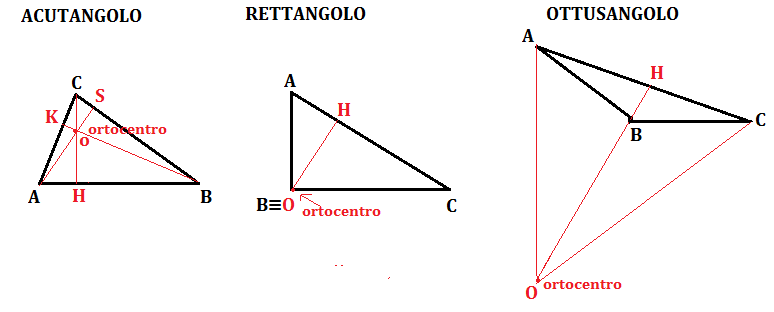
Disegniamo un triangolo acutangolo, un triangolo rettangolo e un triangolo ottusangolo e, in ciascuno di essi tracciamo le tre altezze e e il loro punto d’incontro.
Osserviamo che:
- nel triangolo acutangolo le tre altezze sono sempre interne al triangolo e quindi anche l’ortocentro è interno al triangolo;
- nel triangolo rettangolo due delle tre altezze coincidono con i cateti e i loro piedi coincidono con il vertice dell’angolo retto, l’ortocentro coincide quindi con il vertice dell’angolo retto;
- nel triangolo ottusangolo solo un’altezza è interna, le altre due sono esterne al triangolo e incontrano il lato relativo nel suo prolungamento; l’ortocentro è quindi il punto d’incontro dei prolungamenti delle tre altezze ed è esterno al triangolo.
Riassumendo possiamo dire che: l’altezza di un triangolo relativa ad un lato è la perpendicolare condotta da un vertice al lato opposto o al suo prolungamento.
Le tre altezze di un triangolo si incontrano in un punto detto ortocentro, che è interno nel triangolo acutangolo, esterno nel triangolo ottusangolo, coincidente con il vertice dell’angolo retto nel triangolo rettangolo.