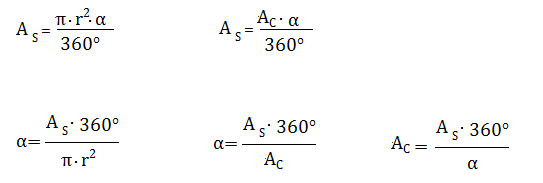Vediamo come si calcola l’Area del settore circolare con una spiegazione semplice, esempi ed esercizi svolti per confrontarsi e capire la risoluzione dei problemi che prevedono l’uso delle proporzioni.
Una volta imparato come mettere in ordine gli elementi della proporzioni, basta conoscere come si svolge senza imparare a memoria tutte le possibili formule si deve applicare solo la regola fondamentale delle proporzioni.
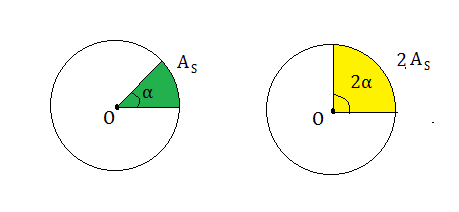
Consideriamo un cerchio di centro O e raggio r e in esso settori circolari di ampiezza α, 2α, 3α…
Raddoppiando o triplicando l’ampiezza, ci accorgiamo che anche l’area del settore circolare corrispondente raddoppia o triplica. Se il settore coincide con tutto il cerchio l’angolo al centro corrispondente diventerà 360°. Quindi le due grandezze, ampiezza dell’angolo al centro α e area del settore circolare sono direttamente proporzionali. Possiamo costruire una tabella di proporzionalità:
| area settore |
ampiezza angolo α |
| α | |
| 2 · |
2 · α |
| 3 · |
3 · α |
| …………. | …………. |
| 360° |
da tale tabella si ottiene la seguente proporzione:
:
= α : 360°
Poichè = π · r² si ottiene:
: π r² = α : 360°
Dalle proporzioni precedenti si ricavano le seguenti formule:
L’area del settore circolare si ottiene dividendo l’area del cerchio a cui appartiene per 360° e moltiplicando il quoziente ottenuto per l’ampiezza del corrispondente angolo al centro espresso in gradi.
Ecco un altro modo per calcolare l’area del settore circolare conoscendo la lunghezza l dell’arco e il raggio r della circonferenza. Dalle proporzioni:
L’area del settore circolare si ottiene dividendo per 2 il prodotto della lunghezza dell’arco e della misura del raggio della circonferenza.