Disegniamo un triangolo acutangolo, rettangolo e ottusangolo e tracciamo le tre bisettrici e l’incentro.
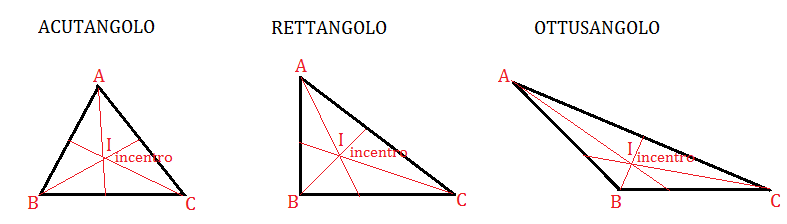
Osserviamo che le tre bisettrici e l’incentro sono sempre interni al triangolo.
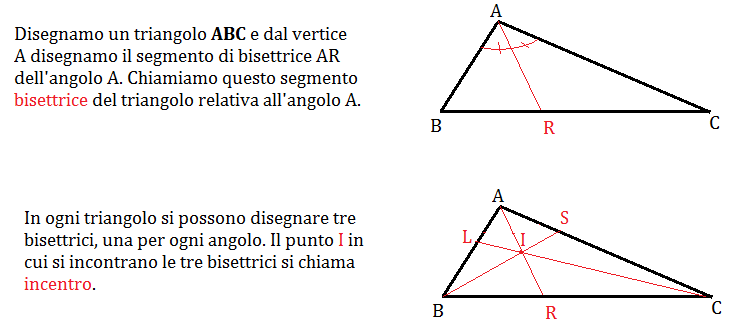
Possiamo riassumere e dire che: la bisettrice di un triangolo relativa a un angolo è il segmento che divide l’angolo compreso tra il vertice dell’angolo stesso e il lato opposto in due angoli uguali.
Le tre bisettrici si incontrano in un punto detto incentro, che è sempre interno al triangolo ed equidistante dai tre lati.