COEFFICIENTE ANGOLARE DI UNA RETTA
L’inclinazione o più precisamente, l’angolo formato dal semiasse positivo dell’asse x e la retta è strettamente legato al coefficiente m della x nell’equazione y=mx.
Per questo il coefficiente m di x è detto coefficiente angolare; al variare di m varia l’inclinazione della retta quindi l’angolo appare tanto minore quanto è più piccolo m.
Se m è positivo la retta si troverà tra il 1° e il 3° quadrante; l’angolo che si forma è acuto.
Se m è negativo la retta si troverà tra il 2 e il 4° quadrante; l’angolo che si forma è ottuso.
Se abbiamo una retta passante per l’origine quindi con l’equazione y=mx vorrà dire che con x≠o m=y\x cioè m è il rapporto tra l’ordinata e l’ascissa.
Consideriamo dei casi;
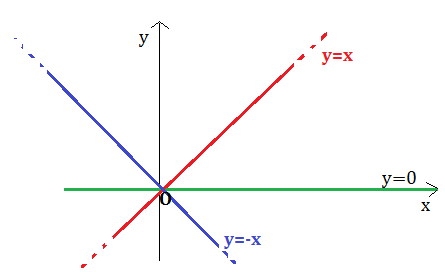
se m=1 l’equazione della retta è: y=x
se m=-1 l’equazione della retta è: y=-x
se m=0 l’equazione della retta è: y=0 cioè la retta coincide con l’asse x
Esercizio n° 1
Data la retta di equazione y = -7x + 2, scrivi le equazioni delle rette parallele e passanti per i punti indicati.
a) Per l’origine
Una retta passante per l’origine è del tipo y = mx e dovendo essere parallela alla retta data, m = – 7, quindi l’equazione della retta richiesta è: y = -7x
b) Per il punto P (0; -6)
L’equazione della retta è del tipo y = mx + q, dovendo essere parallela m = -7; q è l’ordinata del punto d’intersezione con l’asse y, quindi: q = – 6
L’equazione della retta è quindi: y = -7x – 6
Esercizio n° 2
Data la retta di equazione y = – 4x + 1, scrivi le equazioni delle rette perpendicolari e passanti per i punti indicati.
a) Per l’origine
Una retta passante per l’origine è del tipo y = mx e dovendo essere perpendicolare alla retta data avrà:
m = + 1\4
quindi l’equazione della retta richiesta è:
y = + 1\4 x
b) Per il punto P (0; -3)
L’equazione della retta è del tipo y = mx + q, in questo caso abbiamo che:
m = + 1\4 e q = -3
per cui l’equazione della retta è:
y = + 1\4 x – 3