Esercizio di geometria solida
Un triangolo rettangolo ha l’area di 384 cm² e un cateto di 24 cm.
Calcola:
- la misura dell’altezza relativa all’ipotenusa
- l’area laterale, l’area totale e il volume del cono generato dalla rotazione completa del triangolo rettangolo attorno al cateto maggiore
- il rapporto fra l’area laterale del primo cono e l’area laterale del cono generato dalla rotazione completa del triangolo rettangolo attorno al cateto minore.
Equazione
Risolvi la seguente equazione.
Esercizio sul piano cartesiano
Rappresenta i seguenti punti su un piano cartesiano e congiungili nell’ordine dato:
A(-3;2) B(0;6) C(-3;6) D(-6;2)
Qual è il nome del quadrilatero che hai ottenuto? In quale quadrante si trova?
Calcola:
- il perimetro e l’area del quadrilatero (u=1 cm)
- le coordinate del quadrante A’B’C’D’ simmetrico di ABCD rispetto all’asse y
I valori del perimetro e dell’area del nuovo quadrilatero variano rispetto a quelli del primo? Dove si trova adesso il vertice C del quadrante ABCD che prima si trovava alla tua sinistra? In una simmetria assiale, quali sono gli elementi invarianti?
Esercizio sulla probabilità
In un sacchetto vi sono 80 biglietti numerati da 1 a 80. Calcola la probabilità che venga pescato un biglietto il cui numero sia:
- pari e maggiore a 70
- dispari e minore di 30
- multiplo di 11 oppure di 7
Svolgimento
Esercizio di geometria solida
Un triangolo rettangolo ha l’area di 384 cm² e un cateto di 24 cm.
Calcola:
- la misura dell’altezza relativa all’ipotenusa
- l’area laterale, l’area totale e il volume del cono generato dalla rotazione completa del triangolo rettangolo attorno al cateto maggiore
- il rapporto fra l’area laterale del primo cono e l’area laterale del cono generato dalla rotazione completa del triangolo rettangolo attorno al cateto minore.
Equazione
Risolvi la seguente equazione .
4x – 10 + 3 = 4x – 4 – 36x + 18 + 6x – 6
4x – 4x + 36x – 6x =-4 + 18 – 6 + 10 – 3
30x = 15
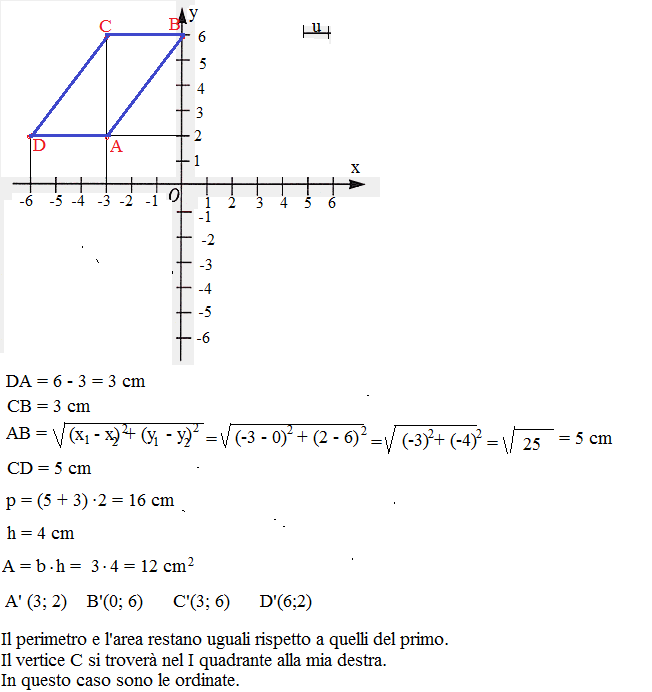
Esercizio sul piano cartesiano
Rappresenta i seguenti punti su un piano cartesiano e congiungili nell’ordine dato:
A(-3;2) B(0;6) C(-3;6) D(-6;2)
Qual è il nome del quadrilatero che hai ottenuto? In quale quadrante si trova?
Calcola:
- il perimetro e l’area del quadrilatero (u=1 cm)
- le coordinate del quadrante A’B’C’D’ simmetrico di ABCD rispetto all’asse y
I valori del perimetro e dell’area del nuovo quadrilatero variano rispetto a quelli del primo? Dove si trova adesso il vertice C del quadrante ABCD che prima si trovava alla tua sinistra? In una simmetria assiale, quali sono gli elementi invarianti?
Esercizio sulla probabilità
In un sacchetto vi sono 80 biglietti numerati da 1 a 80. Calcola la probabilità che venga pescato un biglietto il cui numero sia:
- pari e maggiore a 70 5\80 =1\16
- dispari e minore di 30 15\80=3\16
- multiplo di 11 oppure di 7 17\80 ( il 77 lo si prende una sola volta)