Se consideriamo due insiemi A e B e se tra questi esiste una relazione da A verso B, tale relazione si dice corrispondenza univoca o funzione quando a ogni elemento di A corrisponde uno e un solo elemento di B.
Ricordiamoci che una corrispondenza tra A e B si dice UNIVOCA, quando:
- a un valore di A può corrispondere soltanto un valore di B, e non più di uno;
- ciascun valore di A deve avere un valore corrispondente in B.
Se esiste una funzione tra i due insiemi, si dice che gli elementi di B sono funzione degli elementi di A. Si scriverà :
B =f(A) e si legge che B è funzione di A.
Consideriamo gli insiemi:
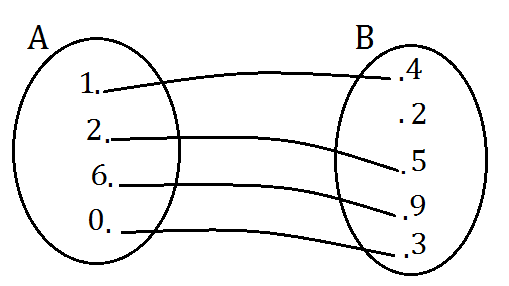
A={ 0,1,2,6}; B={ 2,4,5,9,3}
La rappresentazione di Eurelo-Venn con le frecce visualizza le coppie di elementi corrispondenti nella relazione e indica che la relazione stessa è una funzione.
Possiamo scrivere:
1→4 oppure 4 = f(1);
2→5 oppure 5 = f(2)
Generalizzando possiamo dire che se x è un elemento qualunque dell’insieme di partenza per indicare che y è l’elemento corrispondente dell’insieme di arrivo si usa scrivere:
x→y oppure y=f(x) e questa uguaglianza si legge y è funzione di x.
y è detto l‘immagine di x mediante la funzione f. L’insieme A è detto dominio delle funzione( cioè l’insieme di tutti gli elementi di A che hanno almeno un’immagine in B), il sottoinsieme di B formato dalle immagini degli elementi di A è detto codominio ( cioè l’insieme di tutti gli elementi di B che sono immagini di almeno un elemento di A) che nel nostro caso tale sottoinsieme sarà formato da 3, 4, 5, 9
Per studiare le funzioni è molto utile rappresentarle sul piano cartesiano ed ottenere un grafico:
- sull’asse delle ascisse si rappresenta la variabile indipendente, indicata con la lettera x, scegliendo un’opportuna unità di misura;
- sull’asse delle ordinate si rappresenta la variabile dipendente, indicata con la lettera y, scegliendo un’opportuna unità di misura;
- sul piano si rappresentano i punti aventi come coordinate le coppie di valori corrispondenti secondo la funzione
Una funzione in cui x e y compaiono solo alla potenza di grado 1, si dice funzione di 1° grado.