CONFRONTO TRA FRAZIONI
- Due frazioni sono equivalenti se ridotte ai minimi termini hanno per risultato la stessa frazione irriducibile.
Per esempio 12\15 e 28\35 quindi
le frazioni date quindi sono equivalenti perchè ridotte ai minimi termini hanno per risultato la stessa frazione irriducibile.
Per stabilire se una frazione è maggiore, minore o uguale ad un altra si fanno dei ragionamenti.
- Ogni frazione propria è sempre minore di una frazione impropria 3\7 < 6\5 ; 11\12 <4\3
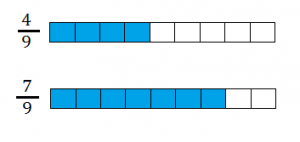
- Date due frazioni con lo stesso denominatore è sempre minore quella con il numeratore minore 4\9 < 7\9. Infatti dividendo due interi nello stesso numero di parti, quindi con la stessa unità frazionaria, vediamo confermato quello già detto.
- Se abbiamo due frazioni proprie per sapere qual è più grande si ridurranno allo stesso denominatore e a quel punto si guarderà il numeratore più grande, allora quella sarà la frazione maggiore 3\4 e 6\7 si trasformeranno in due frazioni con lo stesso denominatore quindi
a questo punto confronteremo il numeratore; il numeratore più grande sarà della frazione più grande 24\27 > 21\28 .
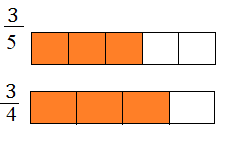
- Due frazioni che hanno lo stesso numeratore 3\7 e 3\4 , sarà maggiore quella con il denominatore minore. Consideriamo le frazioni e rappresentiamole graficamente considerando uno stesso intero. L’unità frazionaria sarà diversa: più piccola quando il denominatore è più grande e anche graficamente si vede che
.
Oltre a tutti questi metodi che possiamo usare per confrontare due frazioni, un altro molto veloce che si può usare è quello del prodotto in croce. Chiamiamo diagonale principale quella in cui si trova il numeratore della prima frazione, diagonale secondaria l’altra.
Se il prodotto sulla diagonale principale è minore di quello sulla diagonale secondaria, la prima frazione è minore della seconda; in caso contrario la prima frazione è maggiore della seconda.
Per esempio confrontiamo 4\9 e 5\12 ; dalla prima diagonale otterremo 4 · 12 = 48, dalla seconda diagonale otterremo 5 · 9 = 45 quindi 48 > 45 dunque 4\9> 5\12.
Lo stesso vale se si considerano i numeri interi, ma il segno meno lo si attribuisce solo ai numeratori. Per esempio confrontiamo – 1\2 e – 2\3 avremo (-1 )·3 = -3 e (- 2 ) · 2 = -4 quindi -3>-4 ⇒- 1\2>- 2\3