Una corrispondenza tra due insiemi A e B si dice univoca se associa a ogni elemento di A uno e un solo elemento di B.
L’espressione “uno e un solo” della definizione sottolinea che devono essere soddisfatte due condizioni:
- per ogni elemento di A esiste un elemento di B associato;
- tale elemento è unico.
Quindi una relazione tra A e B è una funzione se e solo se soddisfa entrambe le condizioni.
Consideriamo due insiemi:
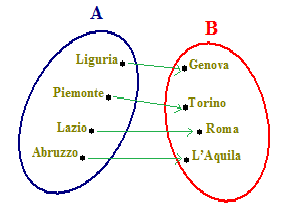
A= { Liguria, Piemonte, Lazio, Abruzzo } l’insieme delle regioni di appartenenza
B = { Genova, Torino, Roma, L’Aquila } l’insieme di quattro città.
Risulta evidente che da ciascun elemento di A parte una sola freccia verso gli elementi di B. Quindi tra i due insiemi esiste una corrispondenza univoca.
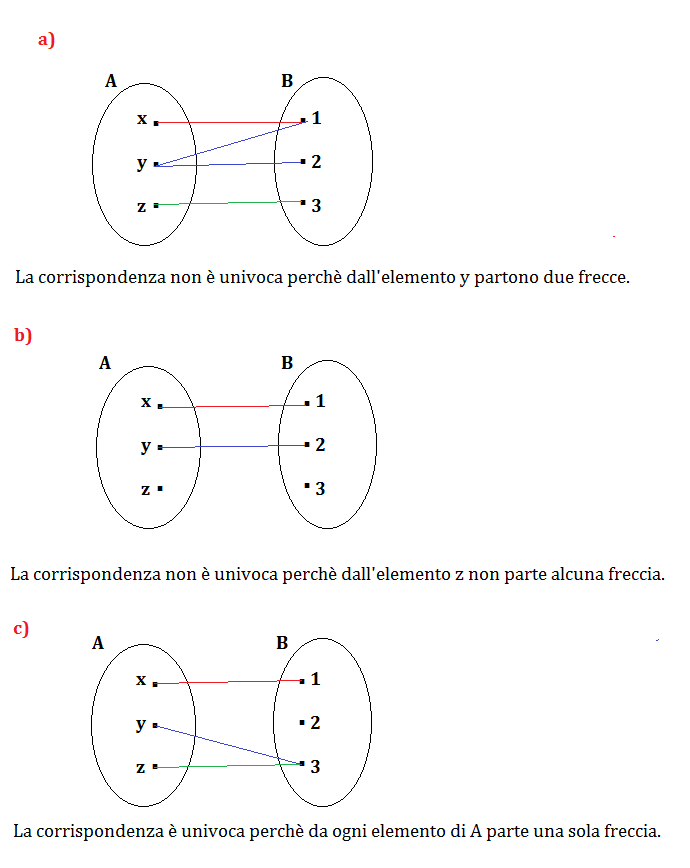
Esercizio
Riconosci la corrispondenza univoca.