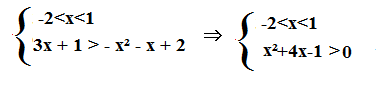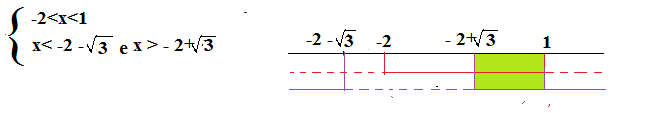Le disequazioni in cui l’incognita compare nel valore assoluto, si risolvono in vari intervalli, come le equazioni dello stesso tipo. Quindi si studia il segno di tutto le parti che stanno in valore assoluto e poi si divide l’insieme R , in cui varia l’incognita, in intervalli. Ovviamente il valore assoluto può assumere il suo valore o l’opposto.
La disequazione assume forme diverse nei vari intervalli e le sue soluzioni sono tutte quelle accettabili delle disequazioni.
Sicuramente un esempio renderà tutto più chiaro:
Esempio
3x + 1 > | x² + x – 2|
Prima di tutto si studia il segno dell’espressione in valore assoluto. Quindi si considera solo x² + x – 2≥0.
A questo punto si trovano le radici che saranno x=-2 e x= 1, poichè la disequazione è maggiore di zero, allora abbiamo soluzioni esterne, quindi x≤-2 e x≥1.
Quindi se facciamo il grafico notiamo che x² + x – 2 è positivo per x≤-2 e x≥1. e negativo per -2<x<1.
A questo punto analizziamo gli intervalli che abbiamo ottenuto. Quelli positivi con quello negativo, e otteniamo:
A questo punto ci andiamo a svolgere singolarmente ogni sistema.
1° sistema
x=1 ± = 1±2 . L e soluzioni saranno
=3 e
= -1
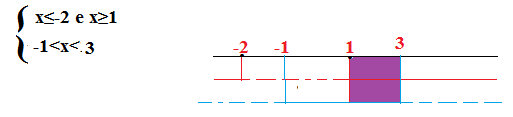
Poichè il delta è maggiore di zero è la disequazione è minore di zero allora si prendono le soluzioni interne. Quindi -1<x<3.
Le soluzioni accettabili, sono quelle dove ci sono solo linee continue e quindi tra 1≤x<3.
2° sistema
Consideriamo l’equazione associata x²+4x-1=0, mi calcolo le soluzioni che sono:
x= – 2 ± quindi
=-2+
e
= -2 –
.
Visto che il delta è maggiore di zero e la disequazione è maggiore di zero allora si considerano le soluzioni esterne, quindi: x< -2 – e x> – 2 +
Quindi:
Le soluzioni accettabili sono – 2 + <x< 1
A questo punto consideriamo le soluzioni finali di tutta la disequazione sono: 1≤x<3 e -2+<x< 1 Le soluzioni possono anche essere unificate e diventa: -2+
<x< 3