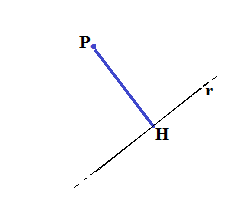
Se consideriamo una retta generica r di equazione ax + by +c e un punto P (;
) esterno a tale retta, la distanza dal punto P alla retta è la misura della perpendicolare PH condotta da P alla retta.
Per calcolare la misura di PH si deve conoscere prima di tutto l’equazione della retta passante per P e perpendicolare a r. Si devono poi conoscere le coordinate del punto H, che è l’intersezione delle due rette. Infine, si calcola la lunghezza di PH con la distanza tra due punti.
Applicando tutti questi passaggi si ottiene la seguente regola:
Si usa il valore assoluto perchè una distanza deve essere sempre positiva. e
sono le coordinate del punto e a, b e c sono i coefficienti della retta.
Consideriamo un esempio per capire meglio.
Calcoliamo la distanza dal punto P (3; -2) dalla retta di equazione 2x – y + 1 =0
Quindi ricapitolando i dati che conosciamo abbiamo:
= 3;
= -2; a = 2; b= -1; c= 1
applicando la formula sopra scritta otteniamo: