La divisione esatta è l’operazione inversa della moltiplicazione.
Infatti il risultato della divisione 15 : 5 è 3 perchè tre è quel numero che moltiplicato per 5 dà per risultato 15.
Analogamente anche 84 : 4= 21 perchè 21 x 4 = 84 divisione propria
Questa divisione si dice divisione esatta.
I numeri 84 e 4 si dicono termini della divisione e più precisamente 84 si dice dividendo e 4 si dice divisore. Il risultato 21 si dice quoziente naturale esatto o quoto.
Il quoziente naturale esatto fra due numeri naturali, di cui il secondo diverso da zero, è quel numero naturale, se esiste, che moltiplicato per il secondo dà per risultato il primo. In questo caso la divisione è detta propria.
La divisione esatta non è sempre possibile nell’insieme N dei numeri naturali e quindi l’insieme N non è chiuso rispetto alla divisione esatta. In questo caso quando il resto non è zero la divisione è detta impropria.
49: 6 = 8 ( resto 1) impropria
LO ZERO E L’UNO NELLA DIVISIONE
- Quando il dividendo è zero, il risultato è sempre zero: 0 : 6 = 0 infatti 6 x 0 = 0
- Quando il divisore è zero, la divisione è impossibile. Non esiste infatti un quoziente che, moltiplicato per 0, dia come risultato un numero diverso da 0: 5 : 0 impossibile .
- Quando il dividendo e il divisore sono zero la divisione è indeterminata, perchè qualunque numero moltiplicato per 0 dà come risultato 0.
- Quando il divisore è 1, il risultato è uguale al dividendo : 5 : 1 = 5.
- Quando si divide un numero per se stesso, il quoziente è 1: 5 : 5 = 1
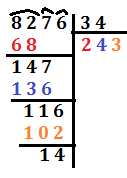
ESEMPIO
8276:34=243 con resto di 14
PROVA DELLA DIVISIONE
Per eseguire la prova della divisione si farà:
dividendo = quoziente esatto per divisore ( se il quoziente è esatto)
dividendo = quoziente x divisore + resto ( se il quoziente è approssimato)
DIVISIONE PROVA
219:3 = 73 (resto 0) 73 x 3=219
326:6 = 54 (resto 2) 54 x 6 + 2 = 324+2 = 326
Mettendo in colonna avremo:
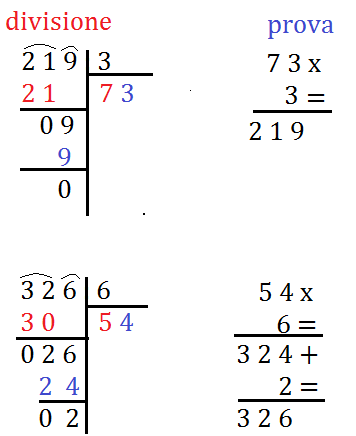
Nel caso il quoziente non sia esatto, la ricerca del risultato può proseguire, calcolando una o più cifre decimali, ottenendo così il quoziente decimale.
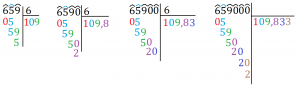
41: 4 = 10 resto 1 659 : 9 = 109 resto 5
Per calcolare il quoziente decimale scriviamo, dopo la cifra delle unità a destra del dividendo, una virgola e tanti zeri quante sono le cifre richieste dall’approssimazione voluta.
Nel quoziente, ottenuto procedendo nel solito modo, si scriverà una virgola prima di abbassare il primo zero delle cifre decimali del dividendo stesso.
Calcoliamo, per esempio, il quoziente fino ai centesimi della divisione 41: 4 e il quoziente fino ai millesimi della divisione 659:6
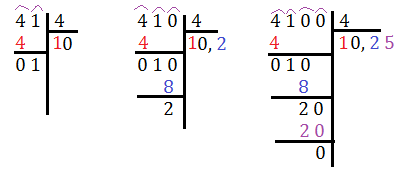
Una volta imparate bene le divisioni si possono fare anche con il modo dell’esempio seguente: