La geometria che adesso tratteremo è detta euclidea, dal nome del grande matematico greco Euclide che fondò lo studio di tutta la geometria sugli enti fondamentali o primitivi, ovvero su tre entità geometriche non definibili ma intuitivamente comprensibili: il punto, la retta e il piano.
IL PUNTO
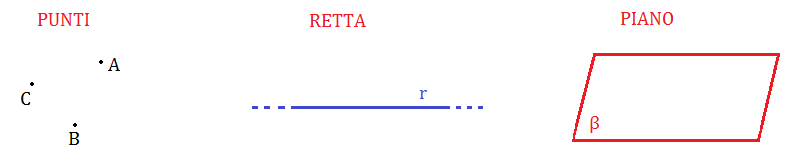
Il punto è il primo ente fondamentale della geometria, è un concetto primitivo privo di effettiva definizione. Esso non ha alcuna dimensione e indica solo una posizione. Per indicare un punto si usa una lettera maiuscola dell’alfabeto.
Per esempio una stella molto lontana vista a occhio nudo, il segno lasciato su un foglio dalla punta ben appuntita di una matita o dalla punta di uno spillo, sono immagini materiali imperfette di un punto geometrico.
LA RETTA
La retta, il secondo ente fondamentale, è immaginabile come un insieme continuo e infinito di punti aventi sempre la stessa direzione. Essa ha una sola dimensione: la lunghezza. Si indica con una lettera minuscola dell’alfabeto.
La retta per esempio la otteniamo facendo scorrere su un foglio la punta di una matita e otteniamo sempre un’immagine imperfetta e incompleta appunto perchè la retta è priva di lunghezza e di spessore e inoltre è illimitata nei due versi.
IL PIANO
Il piano, il terzo ente fondamentale, è immaginabile come un insieme continuo e infinito di rette. Esso ha due sole dimensioni: la lunghezza e la larghezza. Un piano si indica con la lettera minuscola dell’alfabeto greco: α(alfa); β(beta); γ(gamma); δ(delta); ε(epsilon); ζ(zeta); η(eta); θ(teta); ecc.
Sono modelli materiali di piano il pavimento di una stanza, la superficie di un foglio, il piano di un tavolo ecc.