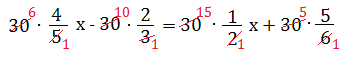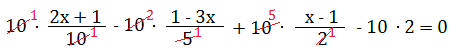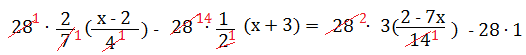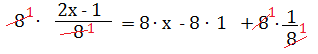Equazioni
Esercizio n° 1
Risolvi le equazioni a coefficienti interi.
a) 3x – 2 + 10 = 4 – 2x + 7x
Si applica la legge del trasporto portando i termini con la x al primo membro e i termini noti al secondo:
3x + 2x – 7x = 4 + 2 – 10
si riducono i termini simili:
– 2x = – 4
si cambiano tutti i segni dei termini:
2x = + 4
si divide per il coefficiente della x:
x = + 4\2 = + 2
b) 2x – 5(x – 4) + 3 = 2(x – 1) + 8
Si eliminano le parentesi svolgendo i calcoli:
2x – 5x + 20 + 3 = 2x – 2 + 8 il 2x si possono eliminare perchè si trova sia al 1° che al 2° membro
– 5x + 20 + 3 = – 2 + 8
si trasportano i termini noti al secondo membro:
– 5x = – 2 + 8 – 20 – 3
si riducono i termini simili:
– 5x = – 17
si cambia di segno:
5x = + 17
si divide per il coefficiente della x:
x = + 17\15
c) 7 – (8x + 2) – 3(3 – 5x) = 4 + 5(2x – 1)
7 – 8x – 2 – 9 + 15x = 4 + 10x – 5
– 8x + 15x – 10x = 4 – 5 – 7 + 2 + 9
-3x = + 3
3x = – 3
x = -3\3 = – 1
d) 3x – [ – 2 (x – 7) + 3x + 9] = 5(2x + 5) + 1 – 4(1 – 3x)
3x – [ – 2x + 14+ 3x + 9] = 10x +25 + 1 – 4 +12x
3x + 2x – 14- 3x – 9 = 10x +25 + 1 – 4 +12x
3x + 2x – 3x – 10x – 12x = +25 + 1 – 4 + 14 + 9
– 20x = 45
20 x= – 45
x = -45\20=-9\4
e) 4x – 2 { – [ -6 (4 – x) + 25 – 5(2x + 3)] } = 3(3 – x) + 8 – 2(x + 4)
4x – 2 { – [- 24 + 6x + 25 – 10x -15] } = 9 – 3x + 8 – 2x – 8
4x – 2 {+ 24 -6x – 25 + 10x +15 } = 9 – 3x + 8 – 2x – 8
4x – 48 +12x +50 -20x – 30 = 9 – 3x + 8 – 2x – 8
4x + 12x -20x +3x +2x = 9 + 8 – 8 + 48 – 50 +30
x = 37
Esercizio n° 2
Risolvi le equazioni a coefficienti frazionari.
a) m.c.m (2; 3 ; 5 ; 6) = 30
24x – 20 = 15x + 25
24x – 15x = 25 + 20
9x = 45
x = 45\9 = 5
b) m.c.m. (2 ; 5 ; 10) = 10
2x + 1 – 2 (1 – 3x) + 5 (x – 1) – 20 = 0
2x + 1 – 2 + 6x + 5x – 5 – 20 = 0
2x + 6x + 5x = – 1 + 2 + 5 + 20
13x = 26
x = 26\13 = 2
c)
m.c.m.(2; 4; 7) = 28
2 (x – 2) – 14 (x + 3) = 6 (2 – 7x ) – 28
2x – 4 – 14x – 42 = 12 – 42x – 28
2x – 14x + 42x = 12 – 28 + 4 + 42
30x = 30
x = 30\30 = 1
d)
m.c.m. = 8
2x – 1 = 8x – 8 + 1
2x – 8x = -8 + 1 +1
– 6x = – 6
6x = + 6
x = 6\6 = 1
e)
m.c.m.(3; 6) = 6
il denominatore si può eliminare come se moltiplicassimo entrambe i membri per 6
– x – 1 = 2x – 4
– x – 2x = + 1 – 4
– 3x = – 3 ⇒ 3x = 3 ⇒ x = 3\3 = +1
Esercizio n° 3
Risolvi le equazioni riducibili a equazioni di 1° grado.
a) (x – 1) (x + 1) – x(x – 2) = 3 (x + 2) + 4 Si eliminano le tonde svolgendo i calcoli
x² – 1 – x² + 2x = 3x + 6 + 4 i termini con x² si possono eliminare:
2x – 3x = 6 + 4 + 1
– x = + 11
x = – 11
b) (2x – 1)² + 1 – 2(3 – x) = – (2x + 1) (2 – x) – 2x ( 1 – x)
4x² – 4x + 1 + 1 – 6 + 2x = – (4x – 2x² + 2 – x) – 2x + 2x²
4x² – 4x + 1 + 1 – 6 + 2x = – 4x + 2x² – 2 + x – 2x + 2x²
Si trasportano i termini con la x al primo membro e i termini noti al 2°:
4x² + 2x – 2x² – x + 2x – 2x² = -2 – 1 – 1 + 6
si riducono i termini simili:
(4 – 2 – 2)x² + (+2 -1 + 2)x = + 2
3x = + 2
x = 2\3
Programma matematica terza media