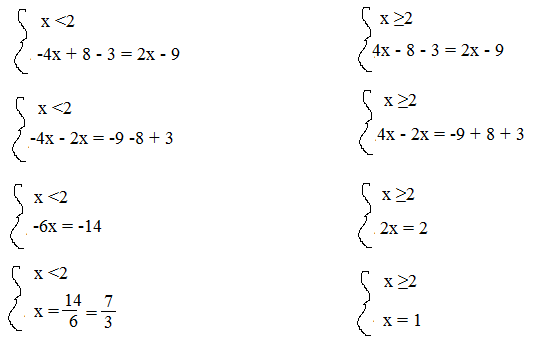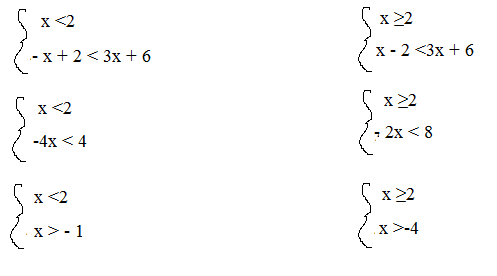Il valore assoluto, chiamato anche modulo, di un numero è il numero considerato senza segno, per esempio |+5| = 5, |-8| = 8.
Ovviamente, se invece del valore assoluto di un numero consideriamo quello di un’espressione con variabili il discorso cambia perchè i valori di x possono essere positivi, negativi o nulli.
Se x ≥ 0 vorrà dire che |x|= x
Se x = +5 allora |x| = |+5| = 5
Se x= 0 |x|=|0| = 0
Se x < 0, dobbiamo scrivere |x|= -x
Se x = -7 allora |x| =|-7| = – (-7) = 7
In definitiva il valore assoluto di una variabile è uguale alla variabile stessa, se essa è positiva o nulla; è uguale all’opposto della variabile se essa è negativa.
Calcoliamo per esempio |x – 3|.
Consideriamo i vari casi:
Se x – 3≥0 quindi x ≥3 allora |x-3| = x – 3
Se x – 3 < 0 quindi x <3 allora il valore assoluto è l’opposto dell’espressione e cioè |x-3|= -(x-3)= -x + 3.
Per risolvere un’equazione che contiene il valore assoluto della variabile, si deve eliminare il valore assoluto, considerando il segno dell’espressione in esso contenuta.
Per esempio:
|4x – 8 | – 3 = 2x – 9
Studiamo prima di tutto il segno all’interno del valore assoluto:
4x – 8 ≥ 0 ⇔ x ≥2 ma se x <2 avremo |4x – 8 |=-(4x – 8) = -4x + 8
Per calcolare i risultati di questa equazione si svolgono due sistemi e cioè con x<2 e x ≥2
7\3 non è accettabile perchè non è minore di 2.
1 non è accettabile perchè non è maggiore di 1.
L’equazione data è impossibile.
Per risolvere una disequazione si deve comparare il valore assoluto dell’incognita, vediamo come si procede.
Per esempio:
|x – 2|< 3x + 6
Anche in questo caso si studia prima il segno all’interno del modulo:
x – 2 ≥ 0 ⇔ x ≥ 2
Se x≥ 2 |x – 2| = x – 2
Se x <2 |x – 2| = – (x-2)= -x + 2
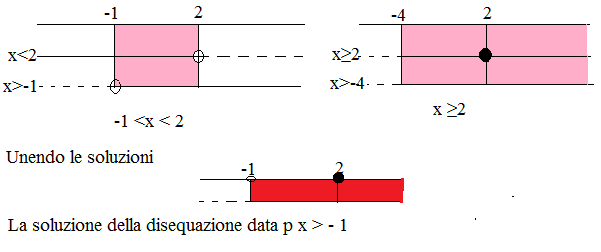
Anche in questo caso la soluzione della disequazione si otterrà dai due sistemi.