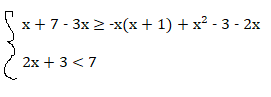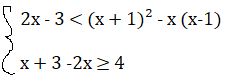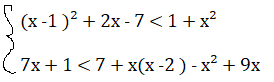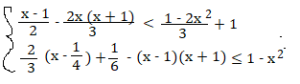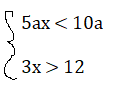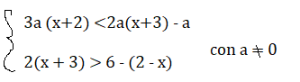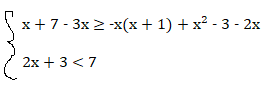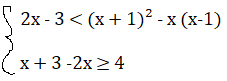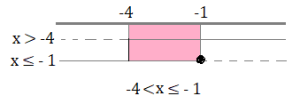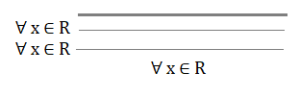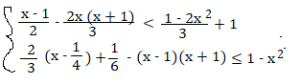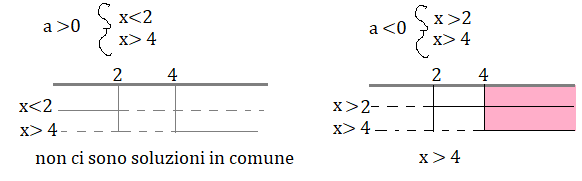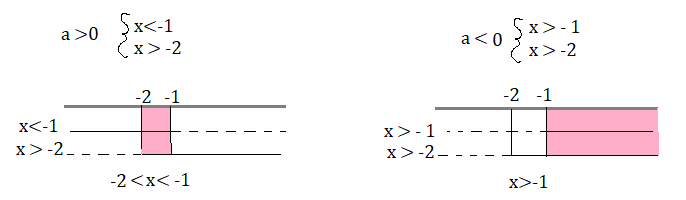Esercizi sui sistemi di disequazioni
Esercizio n° 1
Risolvi il seguente sistema di disequazioni.
Esercizio n° 2
Risolvi il seguente sistema di disequazioni.
Esercizio n° 3
Risolvi il seguente sistema di disequazioni.
Esercizio n° 4
Risolvi il seguente sistema di disequazioni.
Esercizio n° 5
Risolvi il seguente sistema di disequazioni.
Esercizio n° 6
Risolvi il seguente sistema di disequazionia coefficiente letterale.
Esercizio n° 7
Risolvi il seguente sistema di disequazionia coefficiente letterale.
Svolgimento
Esercizio n° 1
Risolvi il seguente sistema di disequazioni.
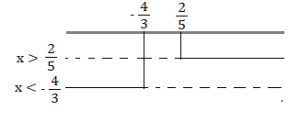
3(1 – x) < 2x + 1 ⇒ 3 – 3x < 2x + 1 ⇒ -3x – 2x < 1 – 3 ⇒ -5x < -2 ⇒ 5x > 2⇒ x > 2\5
2x – 6 > 5x – 2 ⇒ 2x – 5x > -2 + 6 ⇒ -3x > 4 ⇒ 3x < – 4 ⇒ x < -4\3
Rappresentiamo su due rette le due disequazioni.
Non esistono valori di x per cui le disequazioni sono verificate contemporaneamente quindi il sistema è impossibile.
Esercizio n° 2
Risolvi il seguente sistema di disequazioni.
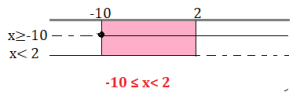
x + 7 – 3x ≥ -x(x + 1) + x² – 3 – 2x ⇒ x + 7 – 3x ≥ –x² – x + x² – 3 – 2x ⇒ x – 3x +x + 2x ≥ – 3 -7 ⇒ x ≥ – 10
2x + 3 < 7 ⇒ 2x < 7 – 3 ⇒ 2x < 4 ⇒ x < 2
Esercizio n° 3
Risolvi il seguente sistema di disequazioni.
2x – 3 < (x + 1)² – x (x-1) ⇒ 2x – 3 < x² + 2x + 1 – x² + x ⇒ 2x -x² – 2x +x²-x< 1 + 3 ⇒ – x < 4 ⇒ x > -4
x + 3 -2x ≥ 4 ⇒x – 2x ≥ 4 – 3 ⇒ -x ≥ 1⇒ x ≤ – 1
Esercizio n° 4
Risolvi il seguente sistema di disequazioni.
(x -1 )² + 2x – 7 < 1 + x² ⇒ x² + 1 – 2x + 2x – 7 < 1 + x² ⇒ -7 <0 ∀ x ∈ R
7x + 1 < 7 + x(x -2 ) – x² + 9x ⇒ 7x + 1 < 7 + x² – 2x – x² + 9x ⇒ 7x +2x – 9x < 7 – 1 ⇒0 < 6 ∀ x ∈ R
Esercizio n° 5
Risolvi il seguente sistema di disequazioni.

⇒
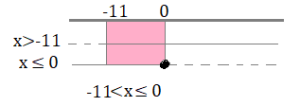
⇒ 3x – 3 – 4x² – 4x – 2 + 4x² – 6 < 0 ⇒-x < +11 ⇒ x>-11





Esercizio n° 6
Risolvi il seguente sistema di disequazioni a coefficiente letterale.
5ax < 10a ⇒

dobbiamo considerare i due casi (a>0 e a<o)poichè abbiamo diviso entrambe i membri per 5a
3x > 12 ⇒ x >4
Il sistema ammette soluzioni solo se a< 0 e l’insieme delle soluzioni è dato da x> 4
Esercizio n° 7
Risolvi il seguente sistema di disequazioni a coefficiente letterale.
3a (x+2) <2a(x+3) – a ⇒ 3ax + 6a < 2ax + 6a – a ⇒ 3ax -2ax <6a – a – 6a ⇒ ax <-a
⇒
2(x + 3) > 6 – (2 – x) ⇒ 2x + 6 > 6 -2 +x ⇒ 2x -x > 6 – 2 – 6 ⇒ x> -2