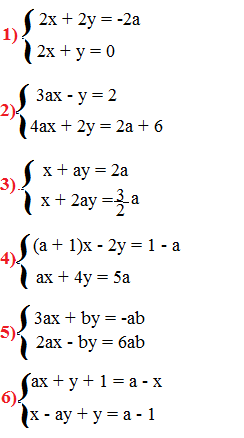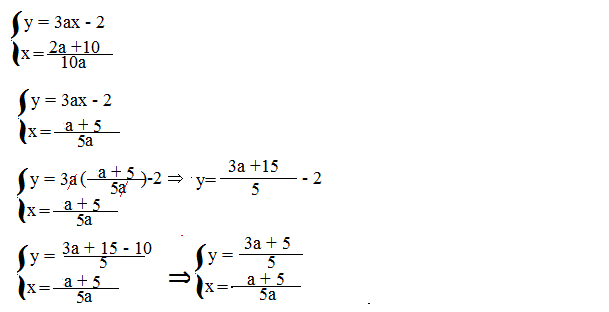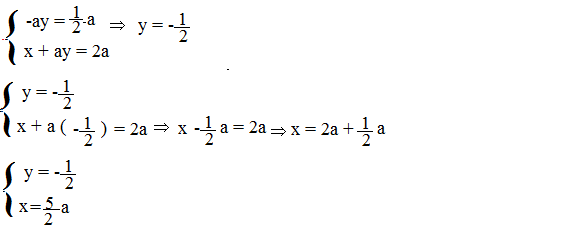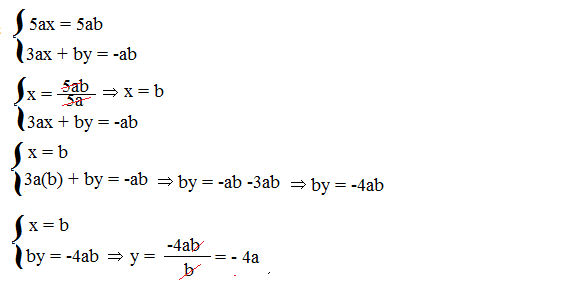Per svolgere gli esercizi sui sistemi letterali bisogna applicare a nostro piacimento le regole imparate per quelli non letterali, quindi possiamo applicare il metodo di sostituzione, Cramer, confronto e riduzione. Importante però è fare la discussione.
Esercizio
Risolvi i seguenti sistemi lineari letterali applicando qualsiasi metodo.
SVOLGIMENTO
La soluzione del sistema è (a; -2a)
Se 10 a= 0 quindi a = 0 e lo vado a sostituire nella seconda equazione ottengo 0= 10 quindi il sistema è impossibile.
Se a ≠ 0 abbiamo
Il sistema ha come soluzioni (;
)
Se a= 0 allora 0•y= 1\2 •0 quindi 0=0 cioè sistema indeterminato.
Se a≠0 abbiamo:
Quindi il sistema è determinato e ha come soluzione (5\2; -1\2)
A questo punto dobbiamo fare la discussione.
Se 6a + 4 = 0 ⇒ a = -4\6 quindi a = -2\3
Sostituendo a nella seconda equazione abbiamo y[6 •(-2\3) + 4] = 6 • (-2\3)² + 4 (-2\3) quindi:
y •0 = 8\3 – 8\3 ⇒ 0 = 0 quindi il sistema per a = -4\6 è indeterminato
Se 6a + 4 ≠ 0 ⇒ a ≠ -4\6 quindi a ≠ -2\3
Il sistema è determinato e la soluzione è ( 1; a)
Se a= 0 ∨ b = 0 il sistema è indeterminato, infatti verrebbe 0=0.
Se a≠0 ∧ b≠0 abbiamo
Il sistema è quindi determinato e ha come soluzione (b; -4a)
A questo punto facciamo la discussione.
Se a= 0 lo andiamo a sostituire nella prima equazione e otteniamo 0•y =0(0 – 1) quindi 0=0.
Se a≠0 abbiamo:
Il sistema quindi è determinato e ha come soluzione (;
)