Esercizio n°1
Un cane legato con una catena lunga 6,0 m corre lungo il percorso circolare con raggio maggiore possibile, compiendo una mezza circonferenza.
Calcola la distanza percorsa e il modulo del vettore spostamento.
Calcola il modulo del vettore spostamento nel caso compia due giri completi.
SVOLGIMENTO
La semicirconferenza quindi sarà proprio uguale alla distanza percorsa e la corda del cane rappresenta il raggio
Quindi avremo che la semicirconferenza sarà = (2 • π • r ): 2, facciamo diviso due appunto per ottenere la semicirconferenza quindi:
d = 2 • 3,14 • 6 : 2 ⇒ d = 18,8 m ≈ 19 m
Il modulo del vettore spostamento non tiene conto del percorso che il cane fa ma è solo il segmento che unisce il punto da cui parte il cane a dove arriva quindi:
vettore spostamento = 2 • r = 12 m
Se il cane compie due giri completi significa che si troverà un’altra volta al punto di partenza quindi lo spostamento è nullo.
Esercizio n°2
Una ragazza prende la rincorsa e sale con il suo skateboard sulla rampa nella figura, partendo dal punto A. Dopo aver percorso la parte semicircolare fino al punto D spicca un salto in verticale di 70 cm, atterra di nuovo sul bordo nel punto D e ritorna indietro fino a fermarsi nel punto B.
Dati del disegno: raggio= 80 cm, distanza dal punto C al punto B 4,5 m, h= 90 cm 3 lunghezza orizzontale tra B ad A 6,2 m
Calcola la distanza totale che percorre lo skateboard prima di fermarsi.
Determina il vettore spostamento e il suo modulo.
SVOLGIMENTO
Dividiamo il percorso in tratti e calcoliamoci prima il tratto AB utilizzando Pitagora poichè il primo tratto è proprio un triangolo rettangolo quindi :
Ovviamente prima dobbiamo fare l’equivalenza e portare i 90 cm a 0,9 m
Il tratto BC è semplice perchè è rettilineo e quindi corrisponde proprio al dato sul disegno quindi 4,5 m.
L’ultimo tratto quindi CD è una semicirconferenza di raggio 80 cm cioè 0,8 m quindi:
A questo punto non ci resta che sommare tutti i valori trovati nei vari tratti e considerando anche il salto di 70 cm quindi 0,7 m ma per due volte perchè ovviamente durante il salto dovrà anche scendere compiendo sempre 0,7 m.
d = 6,26 m + 4,5 m + 2,51 m + 0,7 m + 0,7 m + 2,51 + 4,5 ≈ 21 m
Il vettore spostamento sarà dato dal punto dove parte al punto B e il modulo corrisponde al primo valore calcolato quindi 6,3 m.
Esercizio n°3
Il vettore è scomposto lungo la direzione
e
perpendicolari tra loro. I due vettori componenti così ottenuti hanno modulo
= 10,2 e
= 13,6.
Determina il modulo del vettore .
SVOLGIMENTO
Esercizio n° 4
e lungo la retta verticale .
Calcola i moduli dei due vettori componenti e
.
SVOLGIMENTO
Calcoliamo i moduli delle due componente quindi:
Esercizio n° 5
Un vettore di modulo pari a 4,0 m forma un angolo di 30° con una retta orizzontale.
Calcola la componente orizzontale e quella verticale del vettore.
Quale angolo forma con la retta verticale? (3,5 m; 2,0 m ; 60° )
SVOLGIMENTO
angolo = 90 °- 30° = 60°
Esercizio n° 6
è un vettore lungo che forma un angolo di verso est rispetto alla direzione nord. Moltiplica il vettore
per .
Calcola le componenti del vettore risultante rispetto a un sistema di riferimento cartesiano con l’asse orientato nella direzione sud-nord e l’asse nella direzione ovest-est.
SVOLGIMENTO
verso est
verso nord
verso ovest
verso sud
Esercizio n°7
Il vettore di modulo a = 13 ha componente
= 9 lungo la direzione di un secondo vettore b.
Quanto vale l’angolo tra i vettori a e b?
SVOLGIMENTO
Sappiamo che:
dove α è l’angolo compreso tra i due vettori quindi usando la formula inversa abbiamo:
Esercizio n° 8
Il prodotto scalare tra i vettori e
è è 7.
– Quanto vale la componente di lungo
?
– Puoi determinare il modulo di ?
SVOLGIMENTO
Calcoliamo la componente di b su a considerando il prodotto scalare:
×
=
• a quindi avremo 19 =
• 7 ⇒
= 19 \ 7
Il modulo di b non lo possiamo calcolare perchè mancano dei dati.
Esercizio n° 9
I vettori e
hanno moduli a= 6,82 e b= 9,47 e formano tra loro un angolo di 45°.
Quanto vale il prodotto scalare c= •
?
SVOLGIMENTO
dove α è l’angolo compreso tra i due vettori
Esercizio n° 10
I vettori ed
hanno modulo d= 5,39 ed e= 4,65 e formano tra loro un angolo di 120° . Quanto vale il prodotto scalare k=
•
_
SVOLGIMENTO
Esercizio n° 11
Sono dati i due vettori: =
,
.
Calcola il prodotto scalare tra i due vettori.
SVOLGIMENTO
Esercizio n° 12
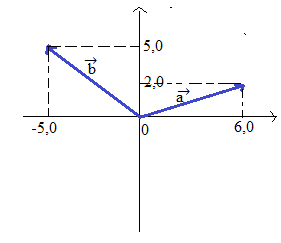
Considera i vettori e
rappresentati nella figura.
Calcola il prodotto scalare dei due vettori.
Determina l’angolo α compreso tra i due vettori. (-20; 117)
SVOLGIMENTO
Il prodotto scalare tra due vettori le cui componenti sono: e
. Il prodotto scalare lo possiamo calcolare come:
= (6; 2)
= (-5, 5)
Esercizio n° 13
Un vettore di modulo a= 31 ha componente
= 11 lungo la direzione di un vettore
di modulo 9,0.
Quanto vale la componente lungo
?
SVOLGIMENTO
Sappiamo che :
dove α è l’angolo compreso tra a e b
Dalla prima ricaviamo il cosα che sarà:
sostituisco il ciò che abbiamo ottenuto nella seconda equazione e otteniamo:
Esercizio n° 14
Il vettore è rivolto verso nord e ha intensità a = 4,0. Il vettore
è rivolto verso est e ha modulo b= 6,5.
Determina il modulo, la direzione e il verso del prodotto vettoriale
SVOLGIMENTO
Il prodotto vettoriale è:
α è l’angolo compreso tra a e b
| ×
|.= ab •senα
Per quanto riguarda la direzione del prodotto vettoriale è sempre perpendicolare ai due vettori, il verso si determina con la regola della mano destra, in questo caso il verso sarà quello che entra dentro il foglio e lo buca.
Il modulo lo calcoliamo come:
| ×
|.= ab •senα = 4,0 • 6,5 • sin 90° = 26
Esercizio n° 15
Sono dati due vettori =(6m)
e
= (4m)
+ (3m)
che hanno la coda nello stesso punto.
Calcola l’area del parallelogramma generato dai due vettori.
Calcola l’area del triangolo che si forma unendo le punte dei vettori.
SVOLGIMENTO
Se andiamo a rappresentare i vettori un piano di assi cartesiani notiamo che essi formeranno un parallelogramma di base 6m ed altezza 3 metri.
L’area del parallelogramma è base per altezza quindi
A = 6 • 3 = 18 m²
Invece per quanto riguarda il triangolo sappiamo che l’area è base per altezza diviso due quindi :
A= 6 • 3 : 2 = 9 m²
Esercizio n° 16
Il vettore è rivolto verso est mentre il vettore
forma con
un angolo di 60° in senso antiorario (cioè verso nord). I loro moduli sono u= 15 e v= 12.
Determina l’intensità, la direzione e il verso del vettore =
×
.
SVOLGIMENTO
Il prodotto vettoriale è pari a :
= 15 • 12 • sen 60° ≈ 160°
Questo è il modulo, per quanto riguarda la direzione sarà quella ortogonale ad entrambi i vettori e quindi quella perpendicolare al nostro foglio e il verso si determina con la regola della mano destra e sarà e quindi sarà quello che entra il foglio.
Esercizio n° 17
Il prodotto vettoriale tra i vettori e
dà un vettore di modulo uguale a 23. L’angolo tra
e
è 20° e
ha modulo pari a 11.
Determina la componente di perpendicolare al vettore
e il modulo di
.
SVOLGIMENTO
Il prodotto vettoriale si calcola nel seguente modo:
| ×
|.= ab •senα
quindi il modulo di b lo possiamo calcolare con la formula inverse:
Per calcolare la componente di perpendicolare al vettore
bisogna considerare la formula per calcolarla che equivale a :
Esercizio n° 18
I due vettori e
hanno modulo rispettivamente 5,0 e 8,0. Il vettore
ha modulo pari a 20.
Calcola l’ampiezza dell’angolo formato dalle direzioni dei due vettori e
.
Il vettore =
×
ha lo stesso modulo di
?
SVOLGIMENTO
Essendo un prodotto vettoriale abbiamo la seguente formula:
quindi
Esercizio n° 19
I vettori e
costituiscono rispettivamente l’ipotenusa e il cateto maggiore di un triangolo rettangolo. Il modulo di
vale 10 e il cateto minore del triangolo è lungo 5,0. Calcola:
L’ampiezza dell’angolo formato dalla direzione dei due vettori;
Il modulo del vettore ;
Il modulo del prodotto vettoriale ×
.
SVOLGIMENTO
In un triangolo rettangolo se un cateto è uguale a metà dell’ipotenusa, ciò implica che sia opposto ad un angolo di 30 gradi.
Oppure un’altra regola è questa:
il cateto è uguale al prodotto dell’ipotenusa e il seno dell’angolo opposto al cateto . Quindi nel caso specifico:
b= a • sen α però a noi serve conoscere l’angolo quindi avremo:
Il modulo del vettore lo calcoliamo con il teorema di Pitagora quindi:
Infine por calcolare il modulo del prodotto vettoriale sappiamo che esso è uguale | ×
|.= ab senα
| ×
.| = 10 •
• sen (30)≈ 44 unità
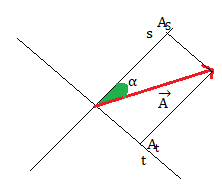
Esercizio n° 20
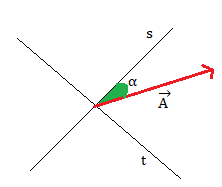
Due rette s e t sono perpendicolari tra loro. Il vettore , di modulo 12, forma un angolo α = 25° con la retta s, come mostra la figura.
Disegna la proiezione di lungo la retta s e t.
Calcola la lunghezza delle proiezioni di lungo le rette s e t.
SVOLGIMENTO
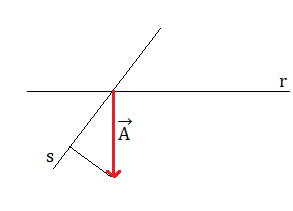
Esercizio n° 21
Le rette r e s formano tra loro un angolo di 120°. Il vettore è perpendicolare a r e ha modulo 8,0.
Determina il modulo della proiezione di lungo le due rette assegnate.
SVOLGIMENTO
La proiezione lungo r è un punto quindi pari a 0, invece quella lungo s è quella disegnata e vale:
il suo angolo sarà 120° dato dal problema – 90° perchè sappiamo che il vettore è perpendicolare quindi l’angolo da considerare è di 30°.
Esercizio n° 22
Due vettori e
hanno modulo rispettivamente pari a 6,2 e 4,5 e formano tra loro un angolo di 65°.
Calcola il loro prodotto scalare usando la componente di su
.
Calcola il loro prodotto scalare con la formula che utilizza i moduli dei vettori e l’angolo compreso tra essi.
SVOLGIMENTO
Esercizio n° 23
I vettori e
hanno moduli A=3,0 e B=4,0 e formano tra loro un angolo di 50°. Calcola il modulo del loro prodotto vettoriale.
SVOLGIMENTO
Il prodotto vettoriale tra due vettori il cui modulo si ricava con la seguente formula:
α è l’angolo formato tra i due vettori.
Esercizio n° 24
I vettori e
hanno moduli A= 7,0 e B= 13 e il modulo del loro prodotto vettoriale è 62.
Calcola l’angolo tra i due vettori.
SVOLGIMENTO
Esercizio n° 25
Il prodotto scalare tra i vettori e
è uguale a 8,0. i moduli dei due vettori dono A= 2,0 e B=5,0.
Calcola il modulo del loro prodotto vettoriale.
SVOLGIMENTO
Prima di tutto scriviamo la formula del prodotto scalare:
ma sappiamo che il prodotto scalare vale 8 quindi abbiamo
8= 2 • 5 cos α quindi cos α = 0,8 ricaviamoci l’angolo con:
Quindi a questo punto conoscendo l’angolo mi posso calcolare il prodotto vettoriale:
Esercizio n° 26
Due vettori e
hanno moduli rispettivamente pari a 3,0 e 4,0 e la proiezione di
su
uguale a 2,0.
Calcola l’angolo compreso tra i due vettori.
Calcola il modulo del prodotto vettoriale ×
.
SVOLGIMENTO
Conoscendo la proiezione significa che conosciamo la componente su
quindi possiamo solo considerare il prodotto scalare per poi calcolarci l’angolo compreso che non conosciamo.
Quindi possiamo dire che :
= 3 • 4 • sen (60°) ≈ 10
Esercizio n° 27
Un vettore forma con l’asse x di un piano cartesiano un angolo di 45°. La sua componente lungo l’asse y è:
.
Calcola il modulo di
SVOLGIMENTO
Sicuramente in questa situazione dobbiamo applicare la regola che dice: che un cateto è uguale al prodotto dell’ipotenusa per il coseno dell’angolo adiacente oppure all’ipotenusa per il seno dell’angolo opposto.
Quindi in questo caso è l’angolo opposto e quindi abbiamo:
Esercizio n° 28
Un vettore forma con l’asse x di un piano cartesiano un angolo di 30° . La sua componente lungo l’asse x è :
Calcola il modulo di B.
SVOLGIMENTO
Sicuramente in questa situazione dobbiamo applicare la regola che dice: che un cateto è uguale al prodotto dell’ipotenusa per il coseno dell’angolo adiacente oppure all’ipotenusa per il seno dell’angolo opposto.
In questo caso siamo nella situazione del cateto e dell’angolo adiacente quindi:
Esercizio n° 29
Le componenti cartesiane di un vettore sono
= 15,0 e
= 30,0.
Calcola il modulo del vettore .
SVOLGIMENTO
In questo caso conoscendo le due componenti il modulo del vettore lo calcoliamo con il teorema di Pitagora.
Esercizio n° 30
I vettori e
hanno modulo A= 1,6 e B = 2,4.
Determina il modulo del vettore somma +
e l’angolo che forma con l’asse x.
SVOLGIMENTO
Prima di tutto ci calcoliamo le componenti di entrambi i vettori:
Il vettore somma lo chiamiamo quindi le sue componenti saranno:
A questo punto ci calcoliamo il modulo di =
Per calcolare l’angolo che il vettore somma forma usiamo la seguente formula:
Esercizio n° 31
Calcola il prodotto scalare dei vettori :
e
SVOLGIMENTO
Prendo le componenti delle x e delle y di entrambi i vettori: