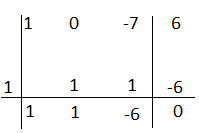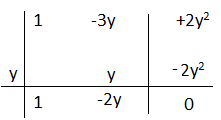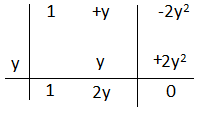Esercizi sul M.C.D. e m.c.m fra polinomi
Esercizio n° 1
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
a³ + 2a² – 3a; 5a³-5a; a² – a³.
Esercizio n° 2
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
x² – xy; xy – y²; x²-y².
Esercizio n° 3
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
8 – x³; 6x² – x³ – 12x + 8; x² – 4x +4.
Esercizio n° 4
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
a³b – 2a²b²; a³-4a²b + 4ab²; a²b² -4 .
.
Esercizio n° 5
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
8x³ – 2x + 1 – 4x²; 4x² – 4x + 1; 1 – 4x².
Esercizio n° 6
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
(x² – 4)(x² + 9); (x³ + 9x)(x²+4x + 4); x³ – 4x
Esercizio n° 7
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
6 – x – x²; x³ – 7x + 6; x² – 3x + 2.
Esercizio n° 8
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
(x – y)(x² – 4y²); x² – 3xy + 2y²; x² + xy -2y²
Svolgimento
Esercizio n° 1
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
a³ + 2a² – 3a; 5a³-5a; a² – a³.
Prima di tutto scomponiamo in fattori i tre polinomi:
1) a³ + 2a² – 3a = a(a² + 2a – 3) il polinomio di secondo grado lo si può ancora scomporre secondo la regola dei particolari trinomi di secondo grado.
Quindi a² + 2a – 3 considerando due numeri la cui somma sia uguale a – 3 e il cui prodotto uguale a +2. I numeri sono +3 e – 1. Quindi:
a(a² + 2a – 3)= a(a + 3)(a – 1)
2) 5a³-5a= 5a(a² – 1) ma il polinomio di secondo grado è scomponibile secondo la regola di somma per differenza. Quindi:
5a³-5a= 5a(a – 1)(a + 1)
3) a² – a³= –a²(a – 1) per rendere questo polinomio uguale agli altri abbiamo messo in evidenza anche il meno.
Quindi:
M.C.D.(a³ + 2a² – 3a; 5a³-5a; a² – a³) = a(a-1);
m.c.m.(a³ + 2a² – 3a; 5a³-5a; a² – a³) =5a²(a + 3)(a – 1)(a+1)
Esercizio n° 2
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
x² – xy; xy – y²; x²-y².
Prima di tutto scomponiamo in fattori i tre polinomi:
1)x² – xy = x(x – y)
2) xy – y²= y(x – y)
3) x²-y²= (x-y)(x+y) →differenza di quadrati
M.C.D.(x² – xy; xy – y²; x²-y²)= x – y
m.c.m.(x² – xy; xy – y²; x²-y²)= xy(x-y)(x+y)
Esercizio n° 3
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
8 – x³; 6x² – x³ – 12x + 8; x² – 4x +4.
Prima di tutto scomponiamo in fattori i tre polinomi:
1)8 – x³= (2 – x)(4 +2x + x²)→somma o differenza di cubi
2)6x² – x³ – 12x + 8 = (2 – x)³→ cubo di un binomio
3) x² – 4x +4 = (2 – x)→ quadrato di un binomio
M.C.D.(8 – x³; 6x² – x³ – 12x + 8; x² – 4x +4)= 2 – x
m.c.m.(8 – x³; 6x² – x³ – 12x + 8; x² – 4x +4)= (2 – x)³(4 +2x + x²)
Esercizio n° 4
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
a³b – 2a²b²; a³-4a²b + 4ab²; a²b² -4.
Prima di tutto scomponiamo in fattori i tre polinomi:
1)a³b – 2a²b²= a²b(a – 2b)
2) a³-4a²b + 4ab²= a(a² – 4ab + 4b²)= a(a -2b)²→quadrato di un binomio
3) a²b² -4 = b²( a² -4b²)= b²(a – 2b)(a + 2b)
M.C.D.(a³b – 2a²b²; a³-4a²b + 4ab²; a²b² -4) = a – 2b
m.c.m.(a³b – 2a²b²; a³-4a²b + 4ab²; a²b² -4)= a²b²(a -2b)²(a + 2b)
Esercizio n° 5
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
8x³ – 2x + 1 – 4x²; 4x² – 4x + 1; 1 – 4x².
Prima di tutto scomponiamo in fattori i tre polinomi:
1)8x³ – 2x + 1 – 4x²=- 4x²(-2x + 1)+ (-2x + 1)= (1 – 2x)(1 – 4x²)= (1 – 2x)²(1 + 2x)
2) 4x² – 4x + 1 = (1-2x)²→ quadrato di un binomio
3) 1 – 4x² = (1 – 2x)(1 + 2x)→ differenza di quadrati
M.C.D.(8x³ – 2x + 1 – 4x²; 4x² – 4x + 1; 1 – 4x²)= 1 – 2x
m.c.m.(8x³ – 2x + 1 – 4x²; 4x² – 4x + 1; 1 – 4x²)= (1 – 2x)²(1 + 2x)
Esercizio n° 6
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
(x² – 4)(x² + 9); (x³ + 9x)(x²+4x + 4); x³ – 4x
Prima di tutto scomponiamo in fattori i tre polinomi:
1)(x² – 4)(x² + 9)= (x-2)(x +2)(x² + 9)
2)(x³ + 9x)(x²+4x + 4)= x(x² + 9)(x + 2)²
3)(x³ – 4x)= x(x² -4)= x(x-2)(x +2)
M.C.D.[(x² – 4)(x² + 9); (x³ + 9x)(x²+4x + 4); x³ – 4x]=x + 2
m.c.m.[(x² – 4)(x² + 9); (x³ + 9x)(x²+4x + 4); x³ – 4x]= x(x² + 9)(x + 2)²(x-2)
Esercizio n° 7
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
6 – x – x²; x³ – 7x + 6; x² – 3x + 2.
Prima di tutto scomponiamo in fattori i tre polinomi:
1)6 – x – x²= -(x² + x – 6) =-(x+3)(x-2)→ scomposizioni di trinomi particolari
2) x³ – 7x + 6;= applico Ruffini
P(1)=1 – 7 + 6 = 0
x³ – 7x + 6= (x – 1)(x² + x – 6)= (x – 1)(x+3)(x-2)
3) x² – 3x + 2 = (x – 2)(x – 1)→ trinomio di secondo grado particolare
M.C.M.(6 – x – x²; x³ – 7x + 6; x² – 3x + 2)= x – 2
m.c.m.(6 – x – x²; x³ – 7x + 6; x² – 3x + 2)= -(x+3)(x-2)(x – 1)
Esercizio n° 8
Determina il M.C.D. e il m.c.m. dei seguenti polinomi.
(x – y)(x² – 4y²); x² – 3xy + 2y²; x² + xy -2y²
Prima di tutto scomponiamo in fattori i tre polinomi:
1)(x – y)(x² – 4y²)=(x – y)(x – 2y)(x + 2y)
2) x² – 3xy + 2y²= applico Ruffini
P(y)= y² – 3y² + 2y² = 0
x² – 3xy + 2y²= (x – y)(x – 2y)
3) x² + xy -2y²= applico Ruffini
P(y)= y² + y² – 2y²=0
quindi x² + xy -2y²=(x + 2y)(x – y)
M.C.D.[(x – y)(x² – 4y²); x² – 3xy + 2y²; x² + xy -2y²]= x – y
m.c.m.[(x – y)(x² – 4y²); x² – 3xy + 2y²; x² + xy -2y²]= (x – y)(x – 2y)(x + 2y)