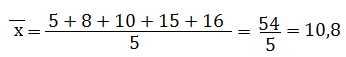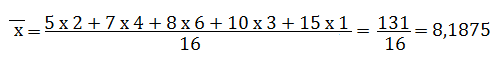Esercizio n°1
Dopo aver svolto un ‘indagine riguardante la colazione degli allievi di una scuola media, il medico scolastico ha ottenuto i seguenti risultati: 120 allievi mangiano latte e biscotti, 25 solo un pezzo di focaccia , 20 mangiano una fetta di torta con succo di frutta, altri 15 bevono solo succo di frutta, 10 mangiano frutta e 10 non mangiano niente.
Dopo aver compilato una tabella di frequenza, determina, per ogni tipo di colazione, la frequenza relativa e individua la moda.
Organizziamo i dati in una tabella riportando oltre alla colonna delle frequenze assolute, quella delle frequenze relative ottenute dividendo la frequenza assoluta di un dato per il totale.
| Frequenza assoluta | Frequenza relativa | |
| Latte e biscotti | 120 | 0,6 |
| Focaccia | 25 | 0,125 |
| Torta e succo di frutta | 20 | 0,1 |
| Succo di frutta | 15 | 0,075 |
| Frutta | 10 | 0,05 |
| Non fa colazione | 10 | 0,05 |
| TOTALE | 200 |
La moda è il valore tra una serie di dati che si presenta con una frequenza maggiore cioè 10
Esercizio n° 2
Per ciascuna successione di dati quantitativi, determina la moda, il campo di variazione e la mediana.
a) 12; 14; 14; 14; 15; 15; 18; 20; 20
I valori sono posti in ordine crescente.
Il valore che compare più volte è il 14, quindi: moda = 14
Il valore minore è 12 e il maggiore è 20, quindi: campo di variazione = 20 – 12 = 8
Ci sono nove valori, quindi quello che occupa la posizione centrale è il quinto a cui corrisponde il valore 15:
mediana = 15
b) 15; 10; 20; 18; 18; 15; 16 ; 22
Disponendo i valori in ordine crescente, la successione diventa: 10; 15; 15; 16; 18; 18; 20; 22
Il 15 e il 18 compaiono entrambi due volte, quindi la distribuzione è bimodale con moda = 15 e 18
Il campo di variazione è = 22-10 = 12
Essendo la successione formata da otto termini, ci sono due valori centrali: il quarto, che è 16 e il quinto che è 18, quindi:
Esercizio n° 3
Per ciascuna successione di dati quantitativi, calcola la media aritmetica.
a) 5; 8; 10; 15; 16
Per calcolare la media aritmetica, si sommano tutti i dati e si divide tale somma per il numero di dati (unità statistiche), in questo caso 5.
b)
| dato | frequenza |
| 5 | 2 |
| 7 | 4 |
| 8 | 6 |
| 10 | 3 |
| 15 | 1 |
La successione di dati quantitativi è assegnata mediante una tabella di frequenza.
Le unità statistiche sono (2, 4, 6, 3, 1) = 16
E’ possibile calcolare la media ponderata, cioè sostituire alle somme di dati uguali , il prodotto del dato per la sua frequenza :