Esercizi sulla lunghezza della circonferenza
Esercizio n°1
Calcola il valore esatto e il valore approssimato per difetto a meno di 1\100 della lunghezza della circonferenza per ciascun caso.
a) d = 27 dm
b) r = 7 cm
Problema n° 2
Si vuole recintare un’aiuola circolare con il raggio di 3,5 m con della rete metallica. Quanti metri di rete occorrono? Se la rete viene venduta in rotoli di 5 m ciascuno, quanti rotoli saranno necessari?
Esercizio n° 3
Calcola la lunghezza del raggio della circonferenza per ciascun caso.
a) C = 78π cm
b) C = 113,04 dm
Problema n° 4
Una circonferenza è lunga 36π cm. Calcola la lunghezza di una circonferenza il cui raggio è 5\6 del raggio della prima.
Problema n° 5
Un triangolo equilatero ha il perimetro di 131,88 cm. Calcola la misura del raggio di una circonferenza la cui lunghezza è uguale a quella del lato del triangolo.
Problema n° 6
Due circonferenze sono lunghe rispettivamente 45π cm e 109,9 cm. Qual è la differenza dei loro raggi?
Problema n° 7
a) Qual è la posizione di una retta rispetto a una circonferenza lunga 75,36 dm, se la sua distanza dal centro è 12 dm.
b) Qual è la posizione reciproca di due circonferenze lunghe rispettivamente 48π cm e 32π cm, sapendo che la distanza tra i loro clienti misura 10 cm?
Problema n° 8
Calcola la lunghezza di una corda di una circonferenza sapendo che dista 5,6 dm dal centro e che la circonferenza è lunga 14π dm.
Problema n° 9
Calcola la lunghezza di una corda di una circonferenza sapendo che una sua corda lunga 9,6 cm, dista 3,6 dal centro.
Problema n° 10
Una circonferenza è lunga 257,48 cm. Calcola la distanza di una corda dal centro sapendo che la corda misura 18 cm.
Problema n° 11
Una circonferenza è lunga 50π cm. Calcola la distanza di due corde parallele situate da parti opposte rispetto al centro e lunghe rispettivamente 48 cm e 40 cm.
Problema n° 12
Un punto P, esterno a una circonferenza, dista 13 cm dal suo centro. Sapendo che la circonferenza è lunga 31,4 cm, calcola l’area del triangolo POA ottenuto tracciando il segmento di tangenza PA.
Problema n° 13
Calcola la lunghezza della circonferenza circoscritta a un rettangolo avente il perimetro di 46 cm e una dimensione lunga 15 cm.
Problema n° 14
Calcola la lunghezza della circonferenza inscritta in un quadrato avente l’area di 225 cm².
Problema n° 15
Un triangolo rettangolo ha i cateti lunghi rispettivamente 39 cm e 52 cm. Calcola la lunghezza della circonferenza circoscritta al triangolo.
Problema n° 16
Data una semicirconferenza di diametro BC, si congiunge un punto qualunque A di essa con i punti B e C , ottenendo così il triangolo rettangolo ABC. Sapendo che la sua area è 57,66 m² e che il cateto AB misura 12,4 m, determina la lunghezza della semicirconferenza.
Problema n° 17
Calcola la misura del contorno della figura formata da un rettangolo e da due semicerchi esterni al rettangolo che hanno per diametri i due lati maggiori, sapendo che le dimensioni del rettangolo sono lunghe rispettivamente 24 cm e 20 cm.
SVOLGIMENTO
Esercizio n°1
Calcola il valore esatto e il valore approssimato per difetto a meno di 1\100 della lunghezza della circonferenza per ciascun caso.
a) d = 27 dm
Il valore esatto è dato da C = π · d. quindi:
C = (π · 27) cm = 27π cm
Il valore approssimato si calcola con la formula C = 3,14 d · quindi:
C = (3,14 · 27) cm= 84,78 cm
b) r = 7 cm
Il valore esatto è dato da C =π · 2r, quindi:
C = ( π · 2 · 7) cm = 14π cm
Il valore approssimato si calcola con la formula C = 3,14 · 2 · r = 6,28 · r, quindi:
C= (6,28 · 7) cm = 43,96 cm
Problema n° 2
Si vuole recintare un’aiuola circolare con il raggio di 3,5 m con della rete metallica. Quanti metri di rete occorrono? Se la rete viene venduta in rotoli di 5 m ciascuno, quanti rotoli saranno necessari?

Esercizio n° 3
Calcola la lunghezza del raggio della circonferenza per ciascun caso.
a) C = 78π cm
Per calcola la lunghezza del raggio si applica la formula , quindi:
b) C = 113,04 dm
Si applica la formula quindi:
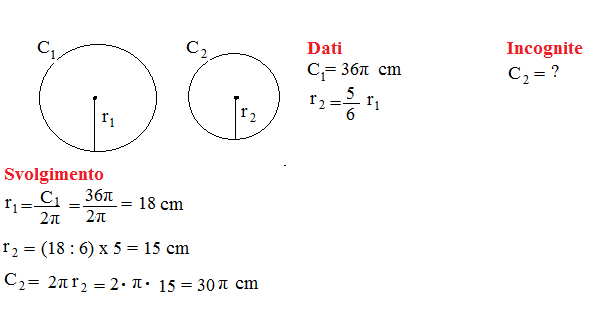
Problema n° 4
Una circonferenza è lunga 36π cm. Calcola la lunghezza di una circonferenza il cui raggio è 5\6 del raggio della prima.
Problema n° 5
Un triangolo equilatero ha il perimetro di 131,88 cm. Calcola la misura del raggio di una circonferenza la cui lunghezza è uguale a quella del lato del triangolo.

Problema n° 6
Due circonferenze sono lunghe rispettivamente 45π cm e 109,9 cm. Qual è la differenza dei loro raggi?

Problema n° 7
a) Qual è la posizione di una retta rispetto a una circonferenza lunga 75,36 dm, se la sua distanza dal centro è 12 dm.
Svolgimento
Per stabilire la posizione della retta rispetto alla circonferenza occorre calcolare la misura del raggio della circonferenza e confrontarla con la distanza della retta dal centro. Si ottiene:
Essendo la distanza dal centro uguale al raggio, la retta è tangente alla circonferenza
b) Qual è la posizione reciproca di due circonferenze lunghe rispettivamente 48π cm e 32π cm, sapendo che la distanza tra i loro clienti misura 10 cm?
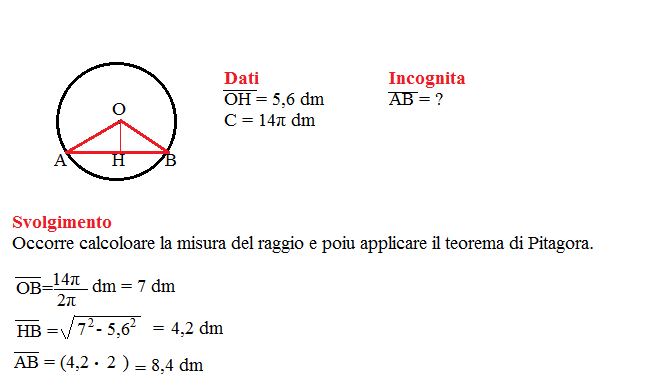
Problema n° 8
Calcola la lunghezza di una corda di una circonferenza sapendo che dista 5,6 dm dal centro e che la circonferenza è lunga 14π dm.
Problema n° 9
Calcola la lunghezza di una corda di una circonferenza sapendo che una sua corda lunga 9,6 cm, dista 3,6 dal centro.

Problema n° 10
Una circonferenza è lunga 257,48 cm. Calcola la distanza di una corda dal centro sapendo che la corda misura 18 cm.

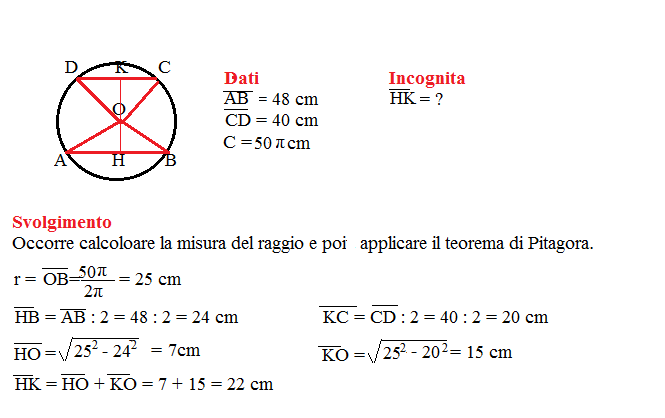
Problema n° 11
Una circonferenza è lunga 50π cm. Calcola la distanza di due corde parallele situate da parti opposte rispetto al centro e lunghe rispettivamente 48 cm e 40 cm.
Problema n° 12
Un punto P, esterno a una circonferenza, dista 13 cm dal suo centro. Sapendo che la circonferenza è lunga 31,4 cm, calcola l’area del triangolo POA ottenuto tracciando il segmento di tangenza PA.

Problema n° 13
Calcola la lunghezza della circonferenza circoscritta a un rettangolo avente il perimetro di 46 cm e una dimensione lunga 15 cm.

Problema n° 14
Calcola la lunghezza della circonferenza inscritta in un quadrato avente l’area di 225 cm².

Problema n° 15
Un triangolo rettangolo ha i cateti lunghi rispettivamente 39 cm e 52 cm. Calcola la lunghezza della circonferenza circoscritta al triangolo.

Problema n° 16
Data una semicirconferenza di diametro BC, si congiunge un punto qualunque A di essa con i punti B e C , ottenendo così il triangolo rettangolo ABC. Sapendo che la sua area è 57,66 m² e che il cateto AB misura 12,4 m, determina la lunghezza della semicirconferenza.

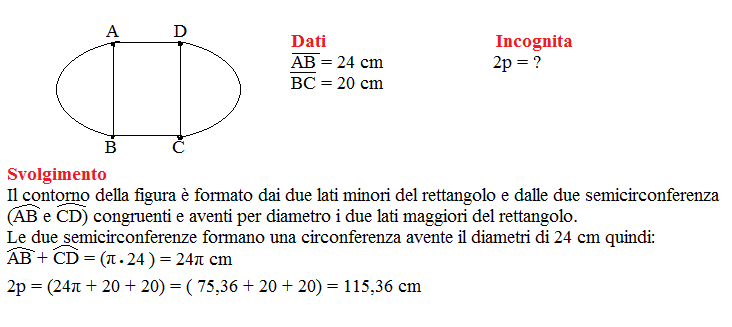
Problema n° 17
Calcola la misura del contorno della figura formata da un rettangolo e da due semicerchi esterni al rettangolo che hanno per diametri i due lati maggiori, sapendo che le dimensioni del rettangolo sono lunghe rispettivamente 24 cm e 20 cm.
Programma geometria terza media