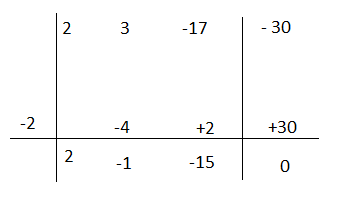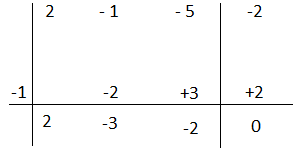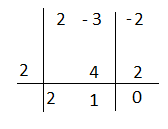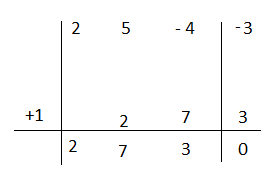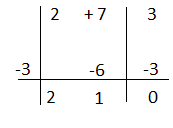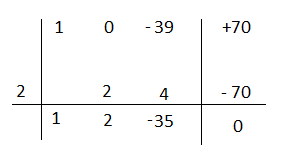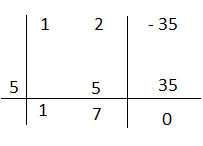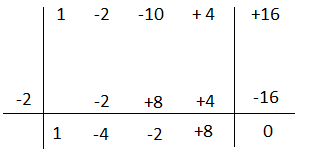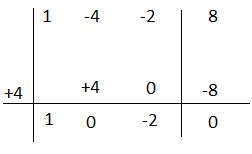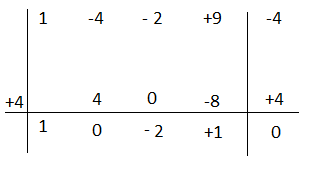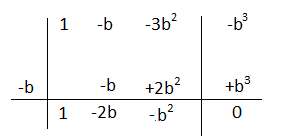Esercizi sulla scomposizione con Ruffini
Esercizio n° 1
Scomporre il polinomio utilizzando la regola di Ruffini.
P(x)= 2x³ + 3x² – 17x – 30
Esercizio n°2
Scomporre il polinomio utilizzando la regola di Ruffini.
P(x)= 2x³ – x² – 5x – 2
Esercizio n°3
Scomporre il polinomio utilizzando la regola di Ruffini.
P(b)= 2b³ +5b² – 4b – 3
Esercizio n°4
Scomporre il polinomio utilizzando la regola di Ruffini.
P(t)= t³ – 39t + 70
Esercizio n°5
Scomporre il polinomio utilizzando la regola di Ruffini.
P(b)= 4b + 16 + – 2b³ – 10b²
Esercizio n°6
Scomporre il polinomio utilizzando la regola di Ruffini.
P(y)= – 4y³ – 2y² +9y – 4
Esercizio n°7
Scomporre il polinomio utilizzando la regola di Ruffini.
P(a)= + 32
Esercizio n°8
Scomporre il polinomio utilizzando la regola di Ruffini.
P(a)= a³ – a²b – 3ab² – b³
Svolgimento
Esercizio n° 1
Scomporre il polinomio utilizzando la regola di Ruffini.
P(x)= 2x³ + 3x² – 17x – 30
Cerchiamo se ci sono dei numeri che annullano il polinomio.
P(+1)= 2(1)³ + 3(1)² – 17(1) – 30 = 2 + 3 -17 – 30= -42≠0
P(-1)= 2(-1)³ + 3(-1)² – 17(-1) – 30 = – 2 +3 + 17 – 30 = -12≠0
P(-2)= 2(-2)³ + 3(-2)² – 17(-2) – 30= -16 + 12 +34 – 30 = 0
Il polinomio quindi è divisibile per x + 2.
2x³ + 3x² – 17x – 30= (x + 2)(2x² – x – 15) ma il polinomio di secondo grado si può ancora scomporre quindi:
P(x)= 2x² – x – 15
P(3)= 2(3)² – 3 – 15 = 18 – 3 – 15 = 0
Applico Ruffini
2x² – x – 15 = (x – 3)(2x + 5)
Unendo i risultati otteniamo che la scomposizione di 2x³ + 3x² – 17x – 30=(x + 2)(x – 3)(2x + 5)
Esercizio n°2
Scomporre il polinomio utilizzando la regola di Ruffini.
P(x)= 2x³ – x² – 5x – 2
P(1)= 2(1)³ – (1)² – 5(1) – 2 = 2 – 1 – 5 – 2 = – 6≠ 0
P(-1)= 2(-1)³ – (-1)² – 5(-1) – 2= -2 -1 +5 – 2 = 0
Il polinomio è quindi divisibile per x +1
(x + 1)(2x² – 3x -2) ma il polinomio di secondo grado si può ancora scomporre.
P(x)=2x² – 3x -2
P(1)= 2(1) – 3(1) – 2 = 2 – 3 – 2 = -3 ≠ 0
P( 2)= 2 (2) – 3(2) – 2 = 4 – 6 – 2 = 0
Il polinomio è divisibile per x – 2.
Applico Ruffini
2x² – 3x -2= (x – 2)(2x + 1)
Unendo tutto avremo che 2a³ – a² – 5a – 2= (x + 1)(x – 2)(2x + 1)
Esercizio n°3
Scomporre il polinomio utilizzando la regola di Ruffini.
P(b)= 2b³ +5b² – 4b – 3
P(1) = 2(1)³ +5(1)² – 4(1) – 3 = 2 + 5 – 4 – 3 = 0
Il polinomio è divisibile per b – 1
Applico Ruffini
2b³ +5b² – 4b – 3= (2b² + 7b + 3)(b – 1) il polinomio di secondo grado si può ancora scomporre.
P(b)=2b² + 7b + 3
P(1)= 2(1)² + 7(1) + 3 = 12
P(-1)= 2(-1)² +7(-1) + 3= 2 – 7 + 3= -2
P(-2)=2(-2)² +7(-2) + 3= 8 – 14 + 3 = -3
P(-3)=2(-3)² + 7(-3) + 3 = 18 – 21 + 3 = 0
Il polinomio è divisibile per b + 3
Applico Ruffini
2b² + 7b + 3= (2b + 1)(b+3)
Unendo i risultati 2b³ +5b² – 4b – 3= (b – 1)(2b + 1)(b+3)
Esercizio n°4
Scomporre il polinomio utilizzando la regola di Ruffini.
P(t)= t³ – 39t + 70
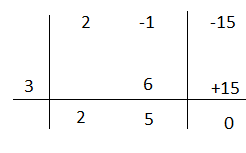
P(2) =(2)³ – 39(2) + 70 = 8 – 78 + 70 = 0
Il polinomio è divisibile per t – 2.
Applico Ruffini
t³ – 39t + 70= (t² + 2t – 35)(t – 2) il polinomio di secondo grado si può ancora scomporre.
P(t)=t² + 2t – 35
P(5)=(5)² +2(5) – 35 = 0
Il polinomio è divisibile per 7 – 5
Applico Ruffini
t² + 2t – 35= (x + 7)(x – 5)
Unendo i risultati t³ – 39t + 70= (t – 2)(x + 7)(x – 5)
Esercizio n°5
Scomporre il polinomio utilizzando la regola di Ruffini.
P(b)= 4b + 16 + – 2b³ – 10b²
P(1)= 4(1) + 16 + – 2(1)³ – 10(1)²= 13
P(2)= 4(2) + 16 + – 2(2)³ – 10(2)² = – 16
P(-2)= 4(-2) + 16 + – 2(-2)³ – 10(-2)² = 0
Il polinomio è divisibile per b + 2.
Prima di applicare Ruffini è importante mettere il polinomio in ordine.
P(b)= – 2b³ – 10b² +4b + 16
Applico Ruffini
– 2b³ – 10b² +4b + 16= (b³ – 4b² – 2b + 8)(b+ 2) il polinomio di terzo grado si può ancora scomporre.
P(b)=b³ – 4b² – 2b + 8
P(1)= 1³ – 4 – 2 + 8 = +3
P(4)= (4)³ – 4(4)² -2(4) + 8 = 64 – 64 – 8 + 8 = 0
Il polinomio è divisibile per b – 4.
Applico Ruffini
b³ – 4b² – 2b + 8= (b² – 2)(b – 4)
Unendo i risultati – 2b³ – 10b² +4b + 16= (b + 2)(b² – 2)(b – 4)
Esercizio n°6
Scomporre il polinomio utilizzando la regola di Ruffini.
P(y)= – 4y³ – 2y² +9y – 4
P(4)= – 4(4)³ – 2(4)² – 4 = 0
Il polinomio è divisibile per y- 4.
Applico Ruffini
– 4y³ – 2y² +9y – 4= (y³ – 2y + 1) (y – 4)il polinomio di terzo grado si può ancora scomporre.
P(y)= y³ – 2y + 1
P(1)= 1 – 2 + 1 = 0
Il polinomio è divisibile per y – 1.
Applico Ruffini
y³ – 2y + 1= (y² +y – 1)(y – 1) il polinomio di secondo grado anche se si fanno vari tentativi si vede che non è divisibile quindi unendo i risultati avremo:
– 4y³ – 2y² +9y – 4= (y – 4)(y² +y – 1)(y – 1)
Esercizio n°7
Scomporre il polinomio utilizzando la regola di Ruffini.
P(a)= + 32
P(-2)= + 32 = -32 + 32 = 0
Il polinomio è divisibile per a + 2
Applico Ruffini
+ 32= (
-2a³ +4a² – 8a + 16)(a + 2) il polinomio facendo i vari tentativi non è divisibile per nulla.
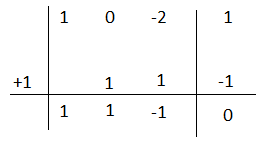
Esercizio n°8
Scomporre il polinomio utilizzando la regola di Ruffini.
P(a)= a³ – a²b – 3ab² – b³
P(-b)=( -b)³ -(- b)²b – 3(-b)b² – b³ = -b³ -b³ +3b³ -b³ = 0
a³ – a²b – 3ab² – b³= (a² – 2ab -b²)(a + b) il polinomio di 2° grado facendo varie prove non è divisibile per nulla.