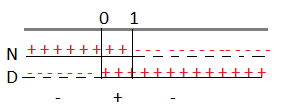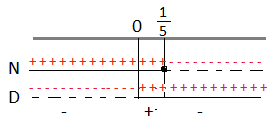Esercizi sulle disequazioni fratte
Esercizio n° 1
Risolvi la seguente disequazione numerica fratta.
Esercizio n° 2
Risolvi la seguente disequazione numerica fratta.
Esercizio n°3
Risolvi la seguente disequazione numerica fratta.
Esercizio n° 4
Risolvi la seguente disequazione numerica fratta.
Esercizio n° 5
Risolvi la seguente disequazione numerica fratta.
Esercizio n° 6
Risolvi la seguente disequazione numerica fratta.
Esercizio n° 7
Risolvi la seguente disequazione numerica fratta.
Esercizio n° 8
Risolvi la seguente disequazione numerica fratta.
Esercizio n° 9
Risolvi la seguente disequazione numerica fratta.
Esercizio n° 10
Risolvi la seguente disequazione letterale fratta.
Esercizio n° 11
Risolvi la seguente disequazione letterale fratta.
Svolgimento
Esercizio n° 1
Risolvi la seguente disequazione numerica fratta.
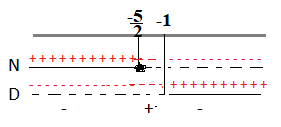
C.E. x + 1 ≠ 0 ⇒ x ≠ – 1
A questo punto si deve studiare il segno della frazione, si studia separatamente il numeratore e il denominatore ponendoli maggiori di zero.
N > 0 ⇔ -2x -5 ≥ 0 ⇒ -2x ≥ 5 ⇒ 2x ≤-5 ⇒ x ≤- 5\2
D > 0 ⇔ 4(x + 1) > 0 ⇒ 4x + 4 > 0 ⇒ 4x > -4 ⇒ x > -1 il denominatore solo maggiore perchè il risultato annulla la disequazione
Riportiamo i risultati sulle rette.
A questo punto consideriamo la disequazione di partenza che è negativa, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli negativi che sono: x < -5\2 e x ≥ -1
Esercizio n° 2
Risolvi la seguente disequazione numerica fratta.
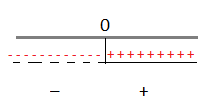
C.E. x ≠0
x > 0
Riportiamo i risultati sulle rette.
A questo punto consideriamo la disequazione di partenza che è negativa, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli negativi che corrispondono a x < 0
Esercizio n°3
Risolvi la seguente disequazione numerica fratta.
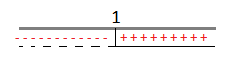
C.E. x – 1 ≠ 0 ⇒ x ≠ 1
x – 1 > 0 ⇒ x > 1
A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono a x > 1
Esercizio n° 4
Risolvi la seguente disequazione numerica fratta.
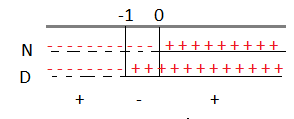
C.E. x ≠ 0
N: x + 1 >0 ⇒ x > – 1
D: x > 0
Riportiamo i risultati sulle rette.
A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono a x < – 1 e x > 1.
Esercizio n° 5
Risolvi la seguente disequazione numerica fratta.
C.-E. 2x ≠ 0 ⇒ x ≠ 0
N: 1 – x ≥ 0 ⇒ -x ≥ – 1 ⇒ x ≤ 1
D: 2x > 0 ⇒ x > 0
Riportiamo i risultati sulle rette.
A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono 0<x ≤ 1
Esercizio n° 6
Risolvi la seguente disequazione numerica fratta.
C.E 2x + 1 ≠ 0 ⇒ x ≠ – 1\2
N: 3x – 6 ≥ 0 ⇒ 3x ≥ 6 ⇒ x ≥ 2
D: 2x + 1 > 0 ⇒ 2x > -1 ⇒ x > – 1\2
Riportiamo i risultati sulle rette.
A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono x < – 1\2 e x ≥ 2
Esercizio n° 7
Risolvi la seguente disequazione numerica fratta.
C.E. x ≠ 0
N : 5 – 25x ≥ 0 ⇒ -25x ≥ – 5 ⇒ 25x ≤ 5 ⇒ x ≤ 1\5
D : x > 0
Riportiamo i risultati sulle rette.
A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono: 0 < x ≤ 1\5
Esercizio n° 8
Risolvi la seguente disequazione numerica fratta.
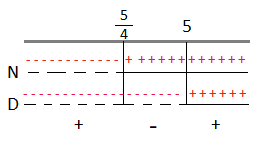
C.E. x – 5 ≠ 0 ⇒ x ≠ 5
N: x² – 5x – 5- (x² + x – 5x – 5 ) + 5x – 5 > 0 ⇒ x² – 5x – 5 –x² – x + 5x + 5 + 5x – 5 > 0⇒ -x +5x- 5> 0
⇒4x >5 ⇒x>5\4
D: 5 (x – 5) > 0 ⇒ x > 5
Riportiamo i risultati sulle rette.
A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono: x < 5\4 e x > 5
Esercizio n° 9
Risolvi la seguente disequazione numerica fratta.
abbiamo usato il meno davanti alla prima frazione per cambiare il segno del denominatore
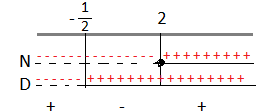
C.E. 3x – 2 ≠ 0 ⇒ x ≠ 2\3
N: 6x² -4x + 2 – (6x² – 4x – 3x + 2) – 12x – 2 > 0 ⇒ 6x² –4x + 2 – 6x² +4x + 3x – 2 – 12x – 2 > 0 ⇒ -9x – 2 > 0 ⇒ 9x+2<0 ⇒ x < – 2\9
D: 2(3x – 2) > 0 ⇒ x >2\3
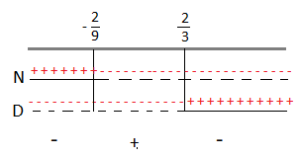
Riportiamo i risultati sulle rette.
A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono: – 2\9< x < 2\3
Esercizio n° 10
Risolvi la seguente disequazione letterale fratta.
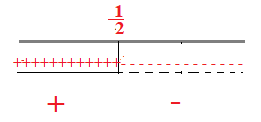
D: -3a(2x-1) > 0 ⇒ 3a(2x-1) < 0 quindi 2x-1< 0
C.E. a≠ 0 quindi per a= 0 la disequazione non ha significato
per a ≠ 0
Le soluzioni saranno quelle negative quindi x > 1\2
Esercizio n° 11
Risolvi la seguente disequazione letterale fratta.
con a> 0
C.E. ≠ -1 e x≠ -a
N: x(a-1) + a² – 1 quindi x(a-1) + (a-1)(a+1) metto in evidenza (a-1)_(x+a+1)
x+a-1 > 0 quindi x> -a -1
D: (x+1)(x+a) > quindi x > -1 e x >-a
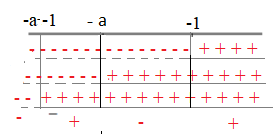
Se a-1 > quindi a > 1
Le soluzioni saranno quelle negative cioè –a< x< -1 e x < -a -1
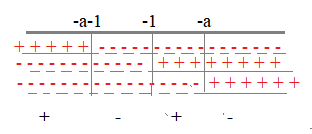
Se a-1 < 0 quindi a < 1
la soluzione del numeratore cambierà di segno e sarà x< -a -1
le soluzioni saranno quelle negative cioè –a – 1< x< -1 e x > -a
Per a= 1 è impossibile
Programma di matematica secondo superiore