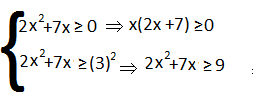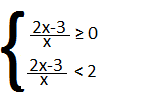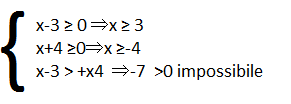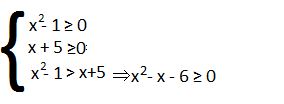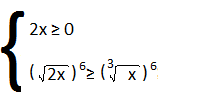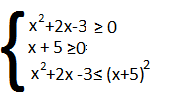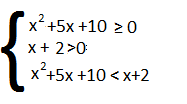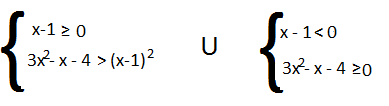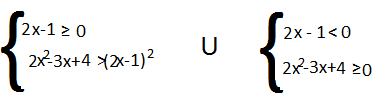Esercizi svolti sulle disequazioni irrazionali, matematica superiori

Esercizi sulle disequazioni irrazionali

Esercizi

Risolvi le seguenti disequazioni irrazionali.

$1) \sqrt{2 x^{2} + 7 x} \geq 3$

$2) \sqrt{\frac{2 x - 3}{x}} < \sqrt{2}$

$3) \sqrt{x - 3} > \sqrt{x + 4}$

$4) \sqrt{x^{2} - 1} > \sqrt{x + 5}$

$5) \sqrt{2 x} \geq \sqrt[3]{x}$

$6) \sqrt{x^{2} + 2 x - 3} \leq x + 5$

$7) \sqrt{x^{2} + 5 x + 10} - 2 < x$

$8) x - 1 < \sqrt{3 x^{2} - x - 4}$

$9) \sqrt{2 x^{2} - 3 x + 4} + 1 > 2 x 9$

SVOLGIMENTO

$1) \sqrt{2 x^{2} + 7 x} \geq 3 q u i n d i i l s i s t e m a p e r r i s o l v e r e l a d i s e q u a z i o n e è :$

Svolgo separatamente le due disequazioni:

x (2x+7)≥0, considero l’equazione associata x(2x+7)=0

quindi x=0 e 2x+7=0⇒ x = – 7\2. La soluzione è x≤-7\2; x ≥0

2x² +7x -9 ≥0, calcoliamoci il Δ= b²-4ac = 49 + 72 = 121 quindi:

$x = \frac{- 7 \pm 11}{4}$

quindi :

$x_{1 =} \frac{- 7 - 11}{4} = - \frac{18}{4} = - \frac{9}{2} p o i x_{2} = \frac{- 7 + 11}{4} = \frac{4}{4} = 1 q u i n d i$ $x \leq - \frac{9}{2}; x \geq 1$

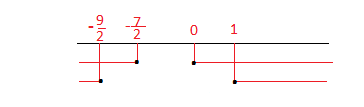
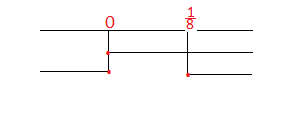
Portiamo i risultati sul grafico:

$x \leq - \frac{9}{2}; x \geq 1$

$2) \sqrt{\frac{2 x - 3}{x}} \leq \sqrt{2} i l s i s t e m a s a r à$

calcolo le due disequazioni separatamente:

$\frac{2 x - 3}{x} \geq 0$

facciamo la regola dei segni:

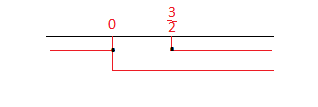
2x-3 ≥ 0 ⇒ x ≥ 3\2

x >0

La soluzione è x ≤0 e x≥ 3\2

$\frac{2 x - 3}{x} < 2$

$\frac{2 x - 3 - 2 x}{x} < 0 \Rightarrow - \frac{3}{x} < 0 \Rightarrow \frac{3}{x} > 0 q u i n d i x > 0$

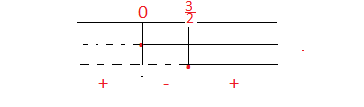
quindi portiamo i valori delle due disequazioni frazionarie sul grafico del sistema e avremo:

$x \geq \frac{3}{2} è l a s o l u z i o n e$

Vediamo l’esercizio successivo

$3) \sqrt{x - 3} > \sqrt{x + 4}$

E’ inutile disegnare il grafico del sistema perchè visto che l’ultima disequazione è impossibile, quindi sul grafico è tratteggiata non ci saranno intervalli con linee continue.

$4) \sqrt{x^{2} - 1} > \sqrt{x + 5}$

Svolgiamo le disequazioni separatamente:

x² – 1≥ 1 l’equazione associata è x² = 1 quindi x = ± 1 quindi x≤-1; x≥ 1
x + 5≥ 0 quindi x ≥ -5
x² – x – 6> 0 Δ= 1 + 24 = 25

$x = \frac{1 \pm 5}{2} q u i n d i x_{1} = \frac{1 + 5}{2} = 3; x_{2} = \frac{1 - 5}{2} = - 2$

Le soluzioni sono esterne quindi: x< -2; x>3

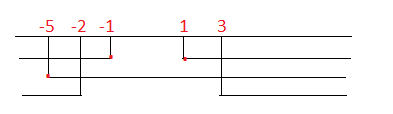
Portiamo le soluzioni delle tre disequazioni nel grafico per i sistema e otteniamo:

$L e s o l u z i o n i s o n o - 5 \leq x < - 2; x > 3$ $5) \sqrt{2 x} \geq \sqrt[3]{x} i l s i s t e m a p e r r i s o l v e r e l a d i s e q u a z i o n e è :$

Svolgiamo le disequaioni separatamente

$\begin{array}{l} x \geq 0 \\ {(2 x)}^{3} \geq x^{2} \Rightarrow 8 x^{3} - x^{2} \geq 0 \Rightarrow x^{2} (8 x - 1) \geq 0 \end{array} \Rightarrow$ $\begin{array}{l} x = 0; x = \frac{1}{8} \Rightarrow x \leq 0; x \geq \frac{1}{8} \end{array}$

Portiamo le soluzioni sul grafico e vediao le soluzioni del sistema:

$L e s o l u z i o n i s o n o x = 0 e x \geq \frac{1}{8}$

Vediamo l’esercizio successivo

$6) \sqrt{x^{2} + 2 x - 3} \leq x + 5$

Svolgiamo le disequazioni separatamente:

x²+2x-3≥ 0 Δ= 4 + 12 = 15

$x = \frac{- 2 \pm 4}{2} q u i n d i x_{1} = \frac{- 2 + 4}{2} = 1; x_{2} = \frac{- 2 - 4}{2} = - 3$ $q u i n d i x \leq - 3; x \geq 1$

x + 5 ≥0 ⇒ x ≥-5
x² + 2x – 3 ≤ (x + 5)² ⇒ x² +2x – 3 ≤ x² + 25 + 10x ⇒ -8x – 28 ≤ 0 ⇒ 8x +28 ≥ 0 quindi x ≥ – 7\2

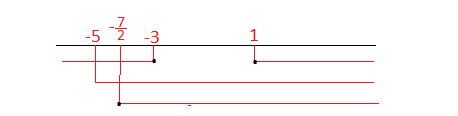
Portiamo i risultati sul grafico:

$L e s o l u z i o n i s o n o - \frac{7}{2} < x \leq - 3; x \geq 1$

$7) \sqrt{x^{2} + 5 x + 10} < x + 2$

Consideriamo le disequazioni separatamente:

x² +5x + 10 ≥ 0 Δ = 25 – 40 = – 15 quindi Δ< 0 disequazione ≥ 0 per ogni x appartenente R
x + 2> 0 ⇒ x > – 2
x² + 5x + 10 < x + 2 ⇒ x² + 4x + 8 < 0 quindi Δ = 16 – 32 = -16 quindi Δ<0 disequazione <0 non ci sono soluzioni.

E’ inutile fare il grafico del sistema perchè la terza disequazione è tratteggiata quindi nessun intervallo avrà tutte le linee continue.

$8) x - 1 < \sqrt{3 x^{2} - x - 4}$

quindi i sistemi per risolverli sono:

Svolgo separatamente i due sistemi.

SISTEMA N° 1

Calcolo separatamente le due disequazioni:

x≥ 1
3x² – x – 4 > x² + 1 – 2x ⇒ 2x² +x -5 > 0

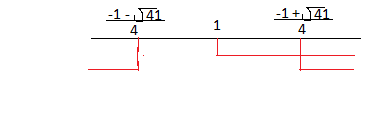
Δ = 1 + 40 = 41

$x = \frac{- 1 \pm \sqrt{41}}{4} q u i n d i x_{1} = \frac{- 1 + \sqrt{41}}{4}; x_{2} = \frac{- 1 - \sqrt{41}}{4}$

le soluzioni del sistema sono:

$\begin{array}{l} x \geq 1 \\ x < \frac{- 1 - \sqrt{41}}{4}; x > \frac{- 1 + \sqrt{41}}{4} \end{array}$

$L a s o l u z i o n e è x > \frac{- 1 + \sqrt{41}}{4}$

Sistema n° 2

x <1
3x² -x-4 ≥0 Δ= 1+48 = 49

$x = \frac{1 \pm 7}{6} q u i n d i x_{1} = \frac{1 + 7}{6} = \frac{4}{3}; x_{2} = \frac{1 - 7}{6} = - 1$

Le soluzioni del sistema quindi sono:

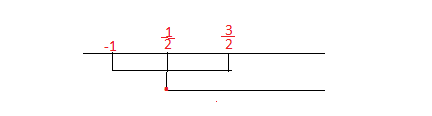
$\begin{array}{l} x < 1 \\ x < - 1; x > \frac{4}{3} \end{array}$

Portiamo le soluzioni sul grafico

$L a s o l u z i o n e è x < - 1$

Unendo le soluzioni dei due sistemi abbiamo :

$x < - 1 \lor x > \frac{- 1 + \sqrt{41}}{4}$

Vediamo l’esercizio successivo

$9) \sqrt{2 x^{2} - 3 x + 4} > 2 x - 1 i s i s t e m i p e r r i s o l v e r e l a d i s e q u a z i o n e s o n o :$

SISTEMA N° 1

x ≥ 1\2
2x² -3x +4 > 4x² + 1 -2x ⇒ 2x² -3x +4 – 4x² – 1 +2x >0

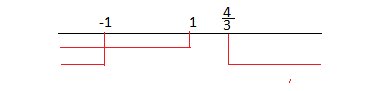
2x² -x-3< 0 Δ= 1 +24=25

$x = \frac{1 \pm 5}{4} q u i n d i x_{1} = \frac{1 + 5}{4} = \frac{3}{2}; x_{2} = \frac{1 - 5}{4} = - 1$

Quindi le soluzioni della disequazione sono -1<x <3\2

$L a s o l u z i o n e è \frac{1}{2} \leq x < \frac{3}{2}$

SISTEMA N° 2

x < 1\2
2x²-3x+4 ≥0 Δ=9-32 = -22 quindi Δ<0 , disequazione maggiore di zero ,per ogni x appartenente a R

La soluzione del secondo sistema è x <1\2.

$D a l l ‘ u n i o n e d e l l e d u e s o l u z i o n i \frac{1}{2} \leq x < \frac{3}{2} e x < \frac{3}{2}$

possiamo scrivere che la soluzione finale è:

Esercizi sulle disequazioni irrazionali

Esercizi

1) 2x2+7x≥3

2) 2x–3x<2

3)x–3>x+4

4)x2 – 1>x+5

5) 2x≥x3

6)x2 + 2x – 3≤x+5

7)x2 + 5x + 10 –2<x

8)x–1 <3x2 –x – 4

9)2x2–3x+4 +1 >2x9

SVOLGIMENTO

1)2x2+7x≥3quindi il sistema per risolvere la disequazione è:

x= –7 ±114

x1=–7–114=– 184= –92 poi x2=–7+114=44=1 quindi x≤–92; x≥1

x≤–92 ; x≥1

2)2x–3x≤2 il sistema sarà

2x–3–2xx<0 ⇒–3x<0 ⇒ 3x>0 quindi x>0

x≥32 è la soluzione

3)x–3>x+4

4)x2 –1 >x+5

x= 1 ± 52 quindi x1= 1+52= 3 ; x2= 1 – 52= –2

Le soluzioni sono –5≤x<–2 ; x>3 5)2x ≥x3 il sistema per risolvere la disequazione è:

x≥0(2x)3≥ x2 ⇒ 8x3– x2≥0 ⇒x2(8x –1)≥0⇒ x=0; x=18⇒ x≤0; x≥18

6)x2+2x–3≤x+5

x= –2 ±42 quindi x1= –2+42= 1; x2= –2–42= –3 quindi x≤–3 ; x≥1

7)x2 + 5x + 10<x +2

8)x – 1 <3x2 – x – 4

x=–1 ±414quindi x1=–1 +414; x2=–1 –414

x≥1x<–1–414; x>–1 + 414

La soluzione è x >–1+414

x=1±76 quindi x1= 1+76=43; x2=1–76= –1

x<1x<–1; x>43

La soluzione è x <–1

x<–1 ∨ x>–1+414

Vediamo l’esercizio successivo

9)2x2 – 3x + 4>2x –1 i sistemi per risolvere la disequazione sono:

x ≥ 1\2

2x² -3x +4 > 4x² + 1 -2x ⇒ 2x² -3x +4 – 4x² – 1 +2x >0

x=1±54 quindi x1=1+54= 32; x2=1–54=–1

La soluzione è 12≤x<32

Dall‘unione delle due soluzioni 12≤x<32 e x <32

x<32

Programma matematica terzo superiore

ImpariamoInsieme

$1) \sqrt{2 x^{2} + 7 x} \geq 3$

$2) \sqrt{\frac{2 x - 3}{x}} < \sqrt{2}$

$3) \sqrt{x - 3} > \sqrt{x + 4}$

$4) \sqrt{x^{2} - 1} > \sqrt{x + 5}$

$5) \sqrt{2 x} \geq \sqrt[3]{x}$

$6) \sqrt{x^{2} + 2 x - 3} \leq x + 5$

$7) \sqrt{x^{2} + 5 x + 10} - 2 < x$

$8) x - 1 < \sqrt{3 x^{2} - x - 4}$

$9) \sqrt{2 x^{2} - 3 x + 4} + 1 > 2 x 9$

$1) \sqrt{2 x^{2} + 7 x} \geq 3 q u i n d i i l s i s t e m a p e r r i s o l v e r e l a d i s e q u a z i o n e è :$

$x = \frac{- 7 \pm 11}{4}$

$x_{1 =} \frac{- 7 - 11}{4} = - \frac{18}{4} = - \frac{9}{2} p o i x_{2} = \frac{- 7 + 11}{4} = \frac{4}{4} = 1 q u i n d i$ $x \leq - \frac{9}{2}; x \geq 1$

$x \leq - \frac{9}{2}; x \geq 1$

$2) \sqrt{\frac{2 x - 3}{x}} \leq \sqrt{2} i l s i s t e m a s a r à$

$\frac{2 x - 3 - 2 x}{x} < 0 \Rightarrow - \frac{3}{x} < 0 \Rightarrow \frac{3}{x} > 0 q u i n d i x > 0$

$x \geq \frac{3}{2} è l a s o l u z i o n e$

$3) \sqrt{x - 3} > \sqrt{x + 4}$

$4) \sqrt{x^{2} - 1} > \sqrt{x + 5}$

$x = \frac{1 \pm 5}{2} q u i n d i x_{1} = \frac{1 + 5}{2} = 3; x_{2} = \frac{1 - 5}{2} = - 2$

$L e s o l u z i o n i s o n o - 5 \leq x < - 2; x > 3$ $5) \sqrt{2 x} \geq \sqrt[3]{x} i l s i s t e m a p e r r i s o l v e r e l a d i s e q u a z i o n e è :$

$\begin{array}{l} x \geq 0 \\ {(2 x)}^{3} \geq x^{2} \Rightarrow 8 x^{3} - x^{2} \geq 0 \Rightarrow x^{2} (8 x - 1) \geq 0 \end{array} \Rightarrow$ $\begin{array}{l} x = 0; x = \frac{1}{8} \Rightarrow x \leq 0; x \geq \frac{1}{8} \end{array}$

$6) \sqrt{x^{2} + 2 x - 3} \leq x + 5$

$x = \frac{- 2 \pm 4}{2} q u i n d i x_{1} = \frac{- 2 + 4}{2} = 1; x_{2} = \frac{- 2 - 4}{2} = - 3$ $q u i n d i x \leq - 3; x \geq 1$

$7) \sqrt{x^{2} + 5 x + 10} < x + 2$

$8) x - 1 < \sqrt{3 x^{2} - x - 4}$

$x = \frac{- 1 \pm \sqrt{41}}{4} q u i n d i x_{1} = \frac{- 1 + \sqrt{41}}{4}; x_{2} = \frac{- 1 - \sqrt{41}}{4}$

$\begin{array}{l} x \geq 1 \\ x < \frac{- 1 - \sqrt{41}}{4}; x > \frac{- 1 + \sqrt{41}}{4} \end{array}$

$L a s o l u z i o n e è x > \frac{- 1 + \sqrt{41}}{4}$

$x = \frac{1 \pm 7}{6} q u i n d i x_{1} = \frac{1 + 7}{6} = \frac{4}{3}; x_{2} = \frac{1 - 7}{6} = - 1$

$\begin{array}{l} x < 1 \\ x < - 1; x > \frac{4}{3} \end{array}$

$L a s o l u z i o n e è x < - 1$

$x < - 1 \lor x > \frac{- 1 + \sqrt{41}}{4}$

$9) \sqrt{2 x^{2} - 3 x + 4} > 2 x - 1 i s i s t e m i p e r r i s o l v e r e l a d i s e q u a z i o n e s o n o :$

$x = \frac{1 \pm 5}{4} q u i n d i x_{1} = \frac{1 + 5}{4} = \frac{3}{2}; x_{2} = \frac{1 - 5}{4} = - 1$

$L a s o l u z i o n e è \frac{1}{2} \leq x < \frac{3}{2}$

$D a l l ‘ u n i o n e d e l l e d u e s o l u z i o n i \frac{1}{2} \leq x < \frac{3}{2} e x < \frac{3}{2}$

$x < \frac{3}{2}$