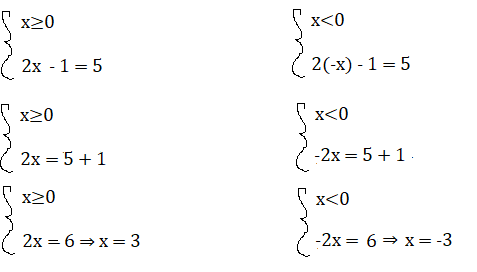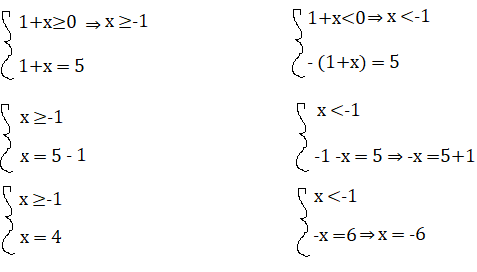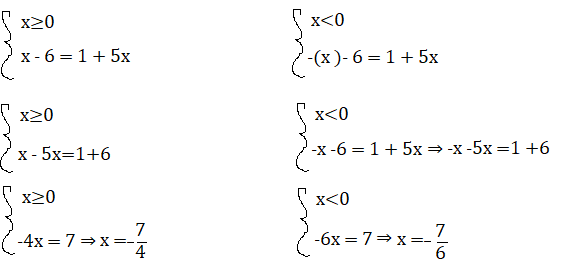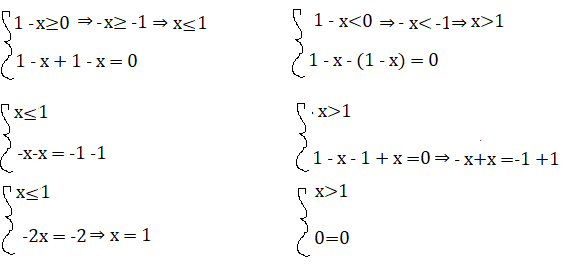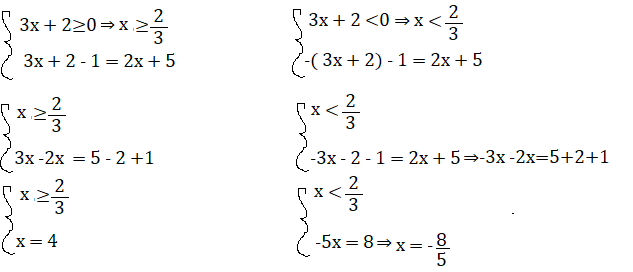Esercizi sulle equazioni e disequazioni con valore assoluto
Esercizio n° 1
Risolvi la seguente equazione con valore assoluto.
2| x | – 1 = 5
Esercizio n° 2
Risolvi la seguente equazione con valore assoluto.
| 1 + x| = 5
Esercizio n° 3
Risolvi la seguente equazione con valore assoluto.
|x | – 6 = 1 + 5x
Esercizio n° 4
Risolvi la seguente equazione con valore assoluto.
1 – x + |1 – x| = 0
Esercizio n° 5
Risolvi la seguente equazione con valore assoluto.
| 3x + 2| – 1 = 2x + 5
Esercizio n° 6
Risolvi la seguente disequazione con valore assoluto.
|3x – 6 | -1 >2(x + 2) – x – 2
Esercizio n° 7
Risolvi la seguente disequazione con valore assoluto.
|1 – x| <6
Esercizio n° 8
Risolvi la seguente disequazione con valore assoluto.
2(1\3 – |x|) <4x – 1
Esercizio n° 9
Risolvi la seguente disequazione con valore assoluto.
Svolgimento
Esercizio n° 1
Risolvi la seguente equazione con valore assoluto.
2| x | – 1 = 5
Essendoci il valore assoluto bisogna analizzare il segno. Consideriamo il sistema per x≥0 e x<0
Per x≥0, x = 3 è una soluzione accettabile perchè appunto è più grande di 0.
Per x<0 , x = – 3 è una soluzione accettabile perchè appunto è minore di 0.
L’equazione quindi avrà due soluzioni x=3 e x= -3.
Esercizio n° 2
Risolvi la seguente equazione con valore assoluto.
| 1 + x| = 5
Essendoci il valore assoluto bisogna analizzare il segno. Consideriamo il sistema per 1+x≥0 e 1+x<0
Per x≥ -1, x= 0 è una soluzione accettabile perchè appunto è più grande di -1
Per x < -1 x = -6 è una soluzione accettabile perchè appunto è minore di -1.
L’equazione quindi avrà due soluzioni x=4 e x= -6.
Esercizio n° 3
Risolvi la seguente equazione con valore assoluto.
|x | – 6 = 1 + 5x
Per x≥0, x = – 7\4 è una soluzione non accettabile perchè non è maggiore di 0.
Per x<0 , x = – 7\6 è una soluzione accettabile perchè appunto è minore di 0.
L’equazione avrà come soluzione solo x= – 7\6
Esercizio n° 4
Risolvi la seguente equazione con valore assoluto.
1 – x + |1 – x| = 0
Per x≥1, x=1 è soluzione
L’equazione avrà come soluzione solo x=1
Esercizio n° 5
Risolvi la seguente equazione con valore assoluto.
| 3x + 2| – 1 = 2x + 5
Per x≥0, x= 4 è soluzione.
Per x<0, x = – 8\5 è soluzione
L’equazione avrà come soluzioni x=4 e x= – 8\5
Esercizio n° 6
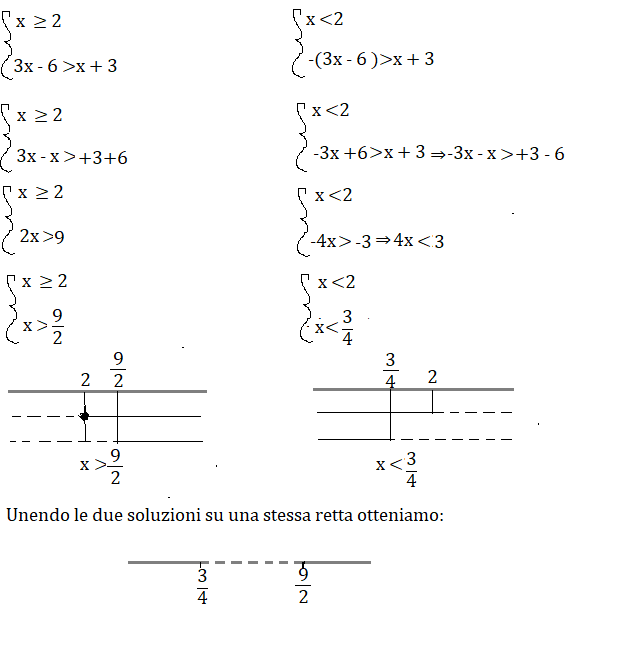
Risolvi la seguente disequazione con valore assoluto.
|3x – 6 | -1 >2(x + 2) – x – 2
Si scriverà la disequazione in modo che la disequazione sia scritta in forma |A|>B.
|3x – 6 |>2x + 4 – x – 2 +1
|3x – 6 |>x + 3
Analizziamo il segno di 3x – 6 e avremo:
3x – 6 ≥0 ⇒ x ≥ 6\3 ⇒ x ≥ 2
La disequazione si divide in due sistemi:
La disequazione ha per soluzioni:
x <3\4 e x >9\2
Esercizio n° 7
Risolvi la seguente disequazione con valore assoluto.
|1 – x| <6
La disequazione ha per soluzione -5 <x<7.
Esercizio n° 8
Risolvi la seguente disequazione con valore assoluto.
2(1\3 – |x|) <4x – 1
2\3 – 2|x|<4x – 1
– 2|x| <4x – 1 -2\3 ⇒ -6|x| <12x -3 -2 ⇒ -6|x| <12x – 5
La disequazione ha per soluzione solo x > 5\18
Esercizio n° 9
Risolvi la seguente disequazione con valore assoluto.