ESERCIZIO N°1
Mario e Luigi spingono una grossa cassa esercitando ciascuno una forza parallela al pavimento, nello stesso verso. La forza risultante sulla cassa è 89 N; Mario spinge con una forza di 35 N.
– Calcola l’intensità della forza sviluppata da Luigi.
– Se Mario e Luigi spingessero in versi opposti, quanto varrebbe la forza risultante sulla cassa?
SVOLGIMENTO
Poichè le forze hanno la stessa direzione ed essendo parallele al pavimento saranno parallele tra loro, inoltre le forze hanno lo stesso verso perchè sia Mario che Luigi stanno spingendo la cassa.
Per la seconda domanda dobbiamo considerare che se i due ragazzi spingessero in senso opposto avremmo che la cassa verrà mossa di più da colui che imprime una forza maggiore quindi Luigi, inoltre avrà anche il suo verso ma modulo dato dalla sottrazione delle forze.
ESERCIZIO N°2
Due rimorchiatori trainano una chiatta con forze di intensità 300 N e 400 N perpendicolari fra loro e applicate allo stesso punto.
Qual è il valore della forza risultante?
SVOLGIMENTO
Poichè le due forze sono perpendicolari tra loro quindi dobbiamo calcolare la forza risultante, quindi il vettore somma con il teorema di Pitagora. Essendo la forza risultante l’ipotenusa del triangolo rettangolo e le due forza sono i cateti.
ESERCIZIO N°3
Due amici spingono un’automobile in panne con due forze parallele e con lo stesso verso, di intensità rispettivamente 250 N e 200 N.
Quanto vale la forza risultante?
Quanto varrebbe la forza risultante se le direzioni delle forze formassero un angolo di 90°?
SVOLGIMENTO
Per quanto riguarda il secondo quesito applichiamo Pitagora
ESERCIZIO N°4
Un fruttivendolo vende le banane a 1,50 € al kilogrammo. Attacca un sacchetto di banane a un dinamometro e legge il valore 20,0 N.
Qual è il costo del sacchetto di banane?
SVOLGIMENTO
Per calcolare il costo del sacchetto di banane bisogna prima di tutto conoscere la massa delle banane, quindi utilizziamo la formula della forza peso.
ESERCIZIO N°5
La spinta del motore di un jet è di circa 7,5 x N. Immaginando di misurarla con un dinamometro, si potrebbe determinare un allungamento l. Misurando invece la forza dei motori di un’astronave, l’allungamento sarebbe circa 400 volte l.
Quale forza produce il motore dell’astronave?
SVOLGIMENTO
L’allungamento della molla di un dinamometro è legata da una relazione di proporzionalità diretta con la forza ad esso attaccata che sta misurando.
Fa= 400 •7,5 x N = 3 ×
N
ESERCIZIO N°6
In una gara di tiro della fune, Paolo, Carlo e Marco esercitano le forze rispettivamente di 560 N, 480 N e 600 N verso sinistra, mentre Franco, Alessandro e Matteo le forze di 550 N, 430 N e 580 N in verso opposto.
Qual è la forza risultante?
SVOLGIMENTO
A questo punto scegliamo un verso positivo, per esempio quello di destra quindi, le forze applicate verso sinistra sono negative.
Quindi il vettore risultante sarà diretto verso sinistra.
ESERCIZIO N°7
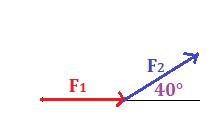
La forza ha direzione orizzontale e modulo 35 N; la forza
, di modulo 50 N ,é inclinata di 40° rispetto all’orizzontale.
Disegna la risultante. Determina il modulo della risultante .
SVOLGIMENTO
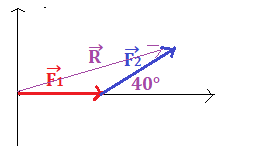
Per determinare la risultante utilizzando il metodo del parallelogramma o il metodo punta-coda. In questo caso potremmo utilizzare quello punta-coda poichè la coda del secondo vettore è posizionato sulla punta del primo.
La risultante è il vettore disegnato.
Prima di tutto calcolo le componenti di lungo l’asse y e l’asse x:
A questo punto mu sommo le componenti delle due forze.
Le componenti di poichè si trova l’ungo l’asse x sono
;
Quindi la somma delle componenti lungo x = 35 N +38,36 N= 73,36 N
Lungo y = 0 + 32,01 N = 32,01 N
Calcoliamo il modulo della risultante con Pitagora.
ESERCIZIO N°8
Appendo il sacchetto del pane al dinamometro, che segna 8,3 N
Quanto pane ho comprato?
SVOLGIMENTO
Per calcolare la massa usiamo la formula inversa della forza peso:
quindi
ESERCIZIO N°9
Su Marte la costante della forza-peso vale g = 3,74 N/kg.
Quanto pesa una confezione di zucchero da 1,00 kg?
SVOLGIMENTO
Poichè
ESERCIZIO N°10
Sulla Terra, un astronauta ha una massa m = 70 kg e un peso P = 687 N.
Se non dimagrisce e non ingrassa, quale sarà la sua massa una volta in orbita?
Cosa puoi dire del suo peso?
SVOLGIMENTO
La massa di un corpo rappresenta la materia di cui esso è formato quindi sarà la stessa in qualsiasi punto dell’universo in cui l’astronauta si trovi, quindi 70 kg. Quella che cambierà sarà la forza peso che dipende dall’accelerazione di gravità che cambia.
ESERCIZIO N°11
Giove è stato studiato da vicino dalla sonda “Galileo”, di massa 2564 kg. Il pianeta è circondato da almeno 67 satelliti naturali, di varie forme e dimensioni, tra i quali sono famosi in particolare lo ed Europa, dove la sonda avrebbe un peso rispettivamente di 4615 N e 3333 N.
Quanto vale g su questi due satelliti?
SVOLGIMENTO
Ci andiamo a calcolare le accelerazioni di gravità di ogni satellite
ESERCIZIO N° 12
Un esploratore ha una massa di 75,0 kg e dall’equatore, dove = 9,78 N/kg, parte per una missione al Polo Nord, dove
=9,83 N/Kg.
Di quanto aumenta il suo peso appena giunto a destinazione?
SVOLGIMENTO
ESERCIZIO N°13
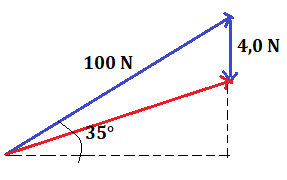
In un calcio di rigore la palla viene lanciata con una forza di 100 N che forma un angolo di 35° con il piano orizzontale. La palla è inoltre sottoposta ad una forza- peso verso il basso di 4,0 N.
Calcola la forza risultante che agisce sulla palla, aiutandoti con la figura.
SVOLGIMENTO
I vettori blu rappresentano la forza applicata al pallone , invece il rosso è il vettore risultante. Creiamo un piano cartesiano in modo che la y è come la forza peso ma verso opposto quindi il modulo della forza peso è -4,0 N.
Le componenti della forza peso saranno lungo l’asse x = 0 , invece lungo l’asse y = -4 N.
Le componenti del vettore blu di 100 N saranno.
Sommiamo le componenti dei due vettori blu, cioè quelle applicate al pallone e otteniamo:
Possiamo calcolare il modulo del vettore somma con Pitagora.
ESERCIZIO N°14
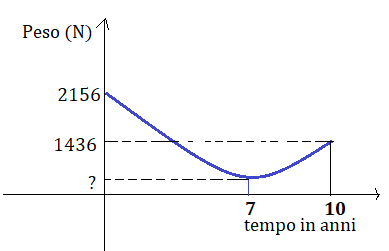
Il grafico della figura rappresenta l’andamento del peso di una sonda che viene lanciata dalla Terra e giunge su un pianeta sconosciuto dopo 10 anni.
Qual è la massa della sonda?
Ricava dal grafico il valore della costante g, del pianeta sconosciuto.
Il valore minimo della costante g durante il viaggio è pari a 1/7 di quello sulla Terra. Completa il grafico con il valore mancante.
SVOLGIMENTO
Visto che all’istante iniziale la sonda si trova sulla terra conosciamo l’accelerazione di gravità pari a 9,8 N\kg. quindi:
Dopo 10 anni la sonda arriva in un altro pianeta di cui non si conosce l’accelerazione di gravità che dovremo calcolare conoscendo la massa che sarà la stessa in qualsiasi parte dell’universo.
Infine il problema afferma che il valore della gravità più basso che la navicella riscontra è 1\7 di quello della terra quindi:
g= 9,8 : 7 = 1,4 N\kg
Per questo valore di g la forza peso è:
ESERCIZIO N°15
Il coefficiente di attrito radente tra una cassapanca di legno di massa 56 kg e il pavimento è 0,27.
Quanto vale l’intensità della forza minima necessaria per mettere in movimento la cassapanca?
SVOLGIMENTO
La forza di attrito statico la calcoliamo come prodotto del coefficiente di attrito statico per la forza perpendicolare che corrisponde alla forza peso.
ESERCIZIO N°16
Vuoi spostare una libreria di massa 90 kg. Il coefficiente di attrito radente dinamico fra la libreria e il pavimento è 0,30.
Qual è l’intensità della minima forza che devi applicare per mantenere in moto la libreria? (2,6 × 1O²N)
SVOLGIMENTO
F =m•g•μ = 90 kg • 9,8 N\kg • 0,30= 256 N critto in notazione scientifica 2,6 × 10² N
ESERCIZIO N°17
Una cassa che pesa 1,3 kN viene spinta sul pavimento da una forza orizzontale. Quando il modulo della forza raggiunge i 2,0 x 10² N, la cassa si mette in moto.
Calcola il coefficiente di attrito statico tra il pavimento e la cassa.
SVOLGIMENTO
Prima di tutto svolgiamo l’equivalenza e portiamo i KN a N quindi moltiplichiamo per 1000 e otteniamo:
ESERCIZIO N°18
Anna sta stirando una maglia di lana. Tiene il ferro da stiro con il braccio inclinato a un angolo di 30° rispetto al piano orizzontale esercitando una forza di 30 N. Il coefficiente di attrito statico in questo caso vale 0,78 e il ferro da stiro ha una massa di 1,2 kg.
Calcola il modulo della forza premente F⊥.
Anna riesce a mettere il ferro da stiro in movimento?
SVOLGIMENTO
Per calcolare la forza perpendicolare dobbiamo tener conto che essa oltre a coincidere con la forza peso, in più bisogna sommare la forza impressa da Anna, quindi la componente perpendicolare della forza impressa da Anna.
Per sapere se Anna riesce a mettere in movimento il ferro da stiro dobbiamo calcolare la forza d’attrito e se questa è minore della componente della forza parallela impressa da Anna allora il ferro si muoverà.
Quindi Anna riesce a muovere il ferro da stiro.
ESERCIZIO N°19
La signora delle pulizie sposta un vaso da fiori di vetro fino a posizionarlo nel centro del piano di un tavolo, anch’esso di vetro (il coefficiente µₛ relativo a vetro su vetro vale 1,0). Il valore della forza al distacco è di 6,0 N.
Qual è la massa del vaso da fiori?
Una volta messo in moto il vaso, la forza di attrito dinamico ha modulo pari a 2,5 N. Ricava il valore del coefficiente di attrito dinamico.
SVOLGIMENTO
Per far muovere un oggetto bisogna vincere la forza di attrito superata la quale l’oggetto comincia a muoversi.
Sappiamo che la formula della forza d’attrito è la seguente:
La formula inversa per calcolare la forza perpendicolare che corrisponde alla forza peso è:
La formula della forza di attrito dinamico è la seguente:
ESERCIZIO N°20
Una cassa di strumenti scientifici di massa 100 kg è stata caricata su un’astronave. L’astronave parte dalla Terra e va a posarsi sulla Luna. Il coefficiente di attrito dinamico fra la cassa e il pavimento dell’astronave è 0,38.
Calcola la forza necessaria per trascinare la cassa prima della partenza e poi sulla Luna.
SVOLGIMENTO
ma la forza peso non la conosciamo ma abbiamo i dati per calcolarcela quindi:
Sulla luna la forza di gravità è diversa infatti g= 1,62 N\Kg
ESERCIZIO N°21
Gianni ha caricato una slitta con le scorte di legna per l’inverno. Per mettere in movimento la slitta esercita una forza di 64 N. I coefficienti di attrito statico e dinamico tra la slitta e la neve ghiacciata sono rispettivamente 0,10 e 0,050.
Qual è la massa della slitta carica?
Quale forza è necessaria per mantenerla in moto una volta partita?
Per riportare nella rimessa la slitta vuota è sufficiente mantenere una forza di 3,4 N. Quanti kg di legna ha
trasportato Gianni?
SVOLGIMENTO
Abbiamo usato il coefficiente d’attrito statico per calcolare la forza per mettere in movimento la slitta
Per rispondere alla seconda domanda dobbiamo calcolare la forza di attrito dinamico quindi considerando l’altro coefficiente quindi:
Con una forza di 3,4 N viene riportata la slitta vuota alla rimessa quindi utilizziamo la formula inversa dalla forza di attrito dinamico poichè la slitta è ancora in movimento quindi:
quindi:
La massa della legna equivarrà al peso trovato all’inizio meno il peso della slitta vuota quindi:
legna= 65 Kg – 7 Kg = 58 Kg
ESERCIZIO N°22
Vuoi tenere sollevato un libro premendolo con la testa contro un muro. Il coefficiente di attrito statico tra il libro e il muro è di 0,55 e il libro ha una massa di 800 g.
Qual è la forza premente in questa situazione?
Quale forza deve essere applicata perpendicolarmente al libro affinché stia fermo?
SVOLGIMENTO
Portiamo gli 800 g in 0,8kg
Poichè il libro si trova poggiato al muro, quindi la forza che determinerà il movimento è la forza peso.
Pe fare in modo che il libro si muova è necessario applicare una forza che si opponga alla forza peso che è la forza di attrito statico
Quindi queste due forze devono essere uguali ed opposte in modo da eguagliarsi quindi:
ESERCIZIO N°23
La molla di un moschettone portachiavi esercita una forza di 0,10 N quando viene compressa di 0,20 cm.
Quanto vale la costante elastica della molla?
SVOLGIMENTO
il meno sta ad indicare che il vettore forza elastica e il vettore allungamento, in questo caso contrazione, hanno verso opposto.
Portiamo i 0,20 cm a 0,002 m , anche il valore del Δx è negativo perchè si comprime, quindi il valore dello spostamento finale meno quello iniziale è negativo perchè la lunghezza finale della molla è minore di quella iniziale.
ESERCIZIO N°24
Le corde di sicurezza che si usano nell’arrampicata sportiva sono elastiche. In una palestra da arrampicata un climber è giunto in alto e si fa calare a terra. La massa dell’alpinista è 70,4 kg e la costante elastica della corda è 3,29 x 10³ N/m.
Calcola l’allungamento subito dalla corda mentre trattiene il climber.
SVOLGIMENTO
La forza che trattiene il climber è la forza elastica della corda
il meno sta ad indicare che il vettore forza elastica e il vettore allungamento, hanno verso opposto.
in questo caso la forza elastica corrisponde con la forza peso perchè è tale forza che tende ad allungare il climber.
la forza elastica è di segno negativo perchè tende ad accorciare la corda.
Oppure potremmo scrivere anche direttamente così :
Il risultato se lo vogliamo portare in cm corrisponde a 21,0 cm
ESERCIZIO N°25
Un lampadario di massa 3,0 kg è appeso a un’asta orizzontale collegata al soffitto da due molle identiche agganciate alle sue estremità. Ciascuna delle molle si allunga di 5,0 cm rispetto alla condizione di equilibrio.
Qual è la costante elastica delle molle se la massa dell’asta è trascurabile?
SVOLGIMENTO
La forza peso dovrà dividersi per le due molle quindi:
Poichè dobbiamo dividere la forza peso per due quindi 14,5 N
quindi in notazione scientifica
ESERCIZIO N°26
Andrea e Antonio vogliono fare una gara di lancio per confrontare le loro fionde. Allungando l’elastico di 8,0 cm la fonda di Andrea esercita una forza elastica di 7,5 N, quella di Antonio di 9,0 N.
Calcola le costanti elastiche dei due elastici.
Di quanto deve allungare l’elastico Andrea per ottenere la stessa forza della fionda di Antonio?
SVOLGIMENTO
Per rispondere alla seconda domanda e quindi di quanto deve allungare Andrea l’elastico per ottenere la stessa forza di Antonio, quindi:
Se volessimo portare il risultato in centimetri otterremo 9,6 cm.
ESERCIZIO N°27
Gigi e Mario spingono un pacco da due parti opposte, uno verso l’altro. Gigi applica una forza di modulo = 56 N, Mario una forza di modulo
= 68 N.
Calcola il modulo e il verso della forza totale applicata al pacco.
SVOLGIMENTO
La direzione delle due forze è la stessa, il verso invece è opposto. Quindi la forza che vincerà sarà quella con modulo maggiore.
ESERCIZIO N°28
Enrica e Giulia sono una di fronte all’altra e tirano due dinamometri attaccati allo stesso oggetto. Il dinamometro di Enrica misura una forza di modulo = (1,4 ± 0,1) N,
quello di Giulia misura = (2,2 ± 0,1) N.
Calcola il modulo della forza totale sull’oggetto e il verso.
SVOLGIMENTO
Le forze esercitate dai due ragazzi sono vettori aventi stessa direzione ma verso opposto quindi la forza risultante =
–
Nella somma o differenza di grandezze con relative incertezze, si sommano o sottraggono le forze risultanti e si sommeranno le incertezze quindi:
=[( 2,2 -1,4)± ( 0,1+0,1)] N = (0,8 ± 0,2 ) N
ESERCIZIO N°29
Un anello di metallo viene tirato da due dinamometri perpendicolari l’uno all’altro. I dinamometri segnano
entrambi una forza di 6,0 N.
Calcola la forza totale applicata all’anello.
SVOLGIMENTO
In questa situazione le due forze sono perpendicolari tra loro e possono essere considerate come le componenti cartesiane della forza risultante applicata all’anello. Quindi la forza la possiamo calcolare con Pitagora.
ESERCIZIO N°30
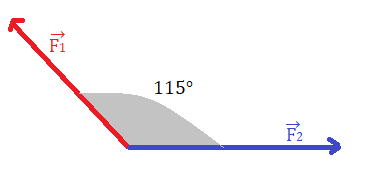
Due cani stanno giocando con un cuscino, tirandolo con i denti in direzioni diverse che formano un angolo di 115°. Entrambi i cani applicano una forza di modulo 41 N.
Calcola il modulo della forza totale applicata al cuscino.
SVOLGIMENTO
Immaginiamo che nel punto d’incontro delle due forse vi sia l’origine di un piano cartesiani , quindi il vettore si troverà sull’asse x. A questo punto le forse le scriviamo come componenti:
=( 41 N; 0)
Le componenti del secondo vettore le calcoliamo come:
= ( -17,3 N ; 37,2 N)
A questo punto applichiamo il teorema di Pitagora per calcolarci il modulo.
ESERCIZIO N°31
Una molla di costante elastica 246 N/m viene compressa di 0,030 m.
Calcola il modulo della forza applicata alla molla.
SVOLGIMENTO
il meno sta ad indicare che il vettore forza elastica e il vettore allungamento, hanno verso opposto.
Il segno meni dell’allungamento sta per il fatto che la molla si comprime. Quindi il risultato è positivo e il vettore della forza elastica è concorde con l’allungamento della molla. Quindi la forza elastica tende ad allungare la molla.
ESERCIZIO N°32
La molla di un dinamometro è lunga 12,0 cm quando è a riposo. Quando il dinamometro misura una forza di modulo 1,0 N, la molla è lunga 12,5 cm.
Calcola la costante elastica della molla.
SVOLGIMENTO
Δx = 12,5 cm – 12,0 cm= 0,5 cm quindi 0,005 cm
Il segno meno della forza elastica è dovuto al fatto che la forza peso tende a far allungare la molla, invece la forza elastica si oppone alla forza peso, quindi ha segno negativo.
ESERCIZIO N°33
Un elastico si comporta come una molla di costante elastica k = 44 Nm.
Di quanto si allunga l’elastico quando viene tirato con una forza di modulo 9,6 N?
SVOLGIMENTO
Il segno meno del risultato ci fa capire che la molla è stata compressa.
ESERCIZIO N°34
Una molla si allunga di 3,6 cm sotto l’azione di una forza F. Se la forza aumenta di 1,4 N, la molla si allunga del 15% in più.
Calcola la costante elastica della molla.
SVOLGIMENTO
Sappiamo che la molla si allunga del 15% quindi 3,6 • 15 : 100= 0,54 cm che corrisponde al Δx che in metri corrisponde a 0,0054. Quindi:
Il modulo della forza elastica l’abbiamo considerato negativo perchè essa continua ad opporsi all’allungamento.
ESERCIZIO N°35
Una molla viene allungata di 3,0 cm quando viene tirata con una certa forza di 15N.
Quando la forza è inferiore del 10%, di quanto e allungata la molla?
SVOLGIMENTO
Con l’allungamento e la forza applichiamo la formula inversa della forza elastica e ci calcoliamo la costante elastica. Prima convertiamo i 3,0 cm in 0,03 m.
La forza elastica è negativa perchè contrasta la forza che tende ad allungarla.
A questo punto il problema ci dice che la forza è inferiore del 10% quindi dobbiamo calcolarci la nuova forza che è uguale a 15 – 10% di 15 = 15 – 1,5 = 13,5 N ( 10% di 15 = 15 •10 : 100)
cioè 2,7 cm
ESERCIZIO N°36
Una cassa contiene 12 kg di arance.
Calcola il peso delle arance.
SVOLGIMENTO
ESERCIZIO N°37
Il peso di una mucca è 4500 N.
Calcola la massa della mucca.
SVOLGIMENTO
ESERCIZIO N°38
Il peso di un’astronauta su Marte è 296,8 N. La costante g su Marte vale 3,72 N/kg
Calcola la massa dell’astronauta.
SVOLGIMENTO
ESERCIZIO N°39
Una roccia su Giove pesa 843,2 N e ha una massa di 34,0 kg.
Calcola la costante di gravità su Giove.
SVOLGIMENTO
ESERCIZIO N°40
Una pietra che si trova su Marte ha una massa di 5,26 kg. La costante g su Marte e 3,72 N/kg.
Calcola la massa di una pietra terrestre che abbia lo stesso peso della pietra che si trova su Marte.
SVOLGIMENTO
ESERCIZIO N°41
Il peso di un oggetto sullo sconosciuto pianeta X è 500N.
La costante g sul pianeta X è il 30% più grande della costante g sul pianeta Y, anch’esso sconosciuto.
Calcola il peso dell’oggetto sul pianeta Y.
SVOLGIMENTO
Sul pianeta X, la massa rimane la stessa, e se g vale il 30% in più, sarà il 130% di quanto vale su Y.
Quindi, per ottenere il peso su Y dobbiamo dividere 500 per 130 e moltiplicarlo per 100.
Otteniamo 384,6 N, che arrotondato dà 385 N
ESERCIZIO N°42
Un giocatore di baseball colpisce una palla di massa 145 g. La forza che la mazza applica alla palla forma un angolo di 30° con la direzione orizzontale ed è diretta verso l’alto. Il modulo della forza è 3,2 N
Calcola il modulo della forza totale applicata alla palla.
SVOLGIMENTO
Le forze che agiscono sulla pallina sono due la forza peso diretta verso il basso e la forza con cui è stata colpita la pallina forma un angolo di 30° con l’asse orizzontale ed è diretta verso l’alto.
Possiamo scomporre le forze nelle loro componenti , quindi la forza = 3,2 N ; le sue componenti sono
= 3,2 • cos 30° = 2,77 N verso destra in avanti;
= 3,2 • sen30° = 1,6 N (verso l’alto);
trovandosi sull’asse delle y avrà ascissa nulla e ordinata uguale al modulo della forza stessa quindi 1,42 N;
x = 2,77 – 0 = 2,77 N
y = 1,6 – 1,42 = 0,18 N (verso l’alto).
applichiamo Pitagora per conoscere il modulo della forza risultante.
ESERCIZIO N°43
Agnese lancia dalla finestra un mazzo di chiavi, di massa 153 g, a Michele. Nel lancio applica una forza di modulo 2,4 N che forma un angolo di 45° con la direzione orizzontale ed è diretta verso il basso.
Calcola il modulo della forza totale applicata al mazzo di chiavi.
SVOLGIMENTO
Sulle chiavi agiscono due forze e cioè la forza peso e la forza impressa da Agnese. Se queste due forze le poniamo all’interno di un piano cartesiano possiamo dire che avranno delle determinate coordinate cartesiane.
Porto i 153 g in 0,153 kg
La forza peso avrà come coordinate (0; 1,5 N)
Le coordinate della forza applicata da Agnese le andiamo a calcolare:
= (1,7 ; 1,7)
La Forza totale sarà data dalla somma delle componenti delle due forze e cioè:
Facciamo Pitagora per conoscere il modulo del vettore risultante
ESERCIZIO N°44
Una cassa di massa m = 8,3 kg giace sul pavimento. Il coefficiente di attrito statico tra la cassa e il pavimento è = 0,32.
Calcola il modulo della forza necessaria a spostare la cassa.
SVOLGIMENTO
ESERCIZIO N°45
Per spostare un masso posto su un piano orizzontale è necessaria una forza di 2480 N. Il coefficiente di attrito
statico tra il masso e il piano è µₛ = 0,12.
Calcola la massa del masso.
SVOLGIMENTO
ESERCIZIO N:46
Un ragazzo applica una forza orizzontale di 48 N a un pacco di massa 16 kg appoggiato sul pavimento. Il coefficiente di attrito statico tra il pacco e il pavimento è 0,35.
Qual è il valore massimo della forza di attrito che il pavimento può esercitare sul pacco?
Il pacco si muove?
Qual è il valore della forza di attrito che agisce sul pacco?
SVOLGIMENTO
Il pacco non si muoverà perchè il ragazzo imprime una forza inferiore a vincere la forza di attrito superata la quale il corpo si muoverebbe.
La forza di attrito è di 48 N
ESERCIZIO N°47
Uno scatolone di massa 40 kg è appoggiato sul pavimento; se si applica una forza orizzontale F di intensità 60 N, lo scatolone non si muove.
Quanto vale la forza di attrito che agisce sullo scatolone?
Lo scatolone comincia a scivolare se, oltre alla forza F, si applica anche una forza Fᵥ diretta verticalmente verso l’alto, di intensità 50 N.
Spiega perché il valore massimo della forza di attrito statico diminuisce.
Quanto vale il coefficiente di attrito statico?
SVOLGIMENTO
La forza di attrito statico è quella forza che si oppone al movimento iniziale di un oggetto. Se lo scatolone non si muove nonostante la forza applicata, significa che la forza di attrito statico sta bilanciando la forza applicata, mantenendo lo scatolone in uno stato di equilibrio.
La forza premente è la forza verticale netta che agisce su uno scatolone. È data dalla forza peso meno qualsiasi forza verticale applicata verso l’alto. In questo caso, la forza premente è diminuita a causa della forza verticale applicata verso l’alto, riducendo così anche la forza di attrito massima che può agire sullo scatolone.
Il valore della forza di attrito statico diminuisce perchè è direttamente proporzionale alla forza premente cioè la forza perpendicolare.