ESERCIZIO N°1
Un lampadario di massa 3,5 kg è in equilibrio appeso al soffitto.
Disegna le forze che agiscono sul lampadario.
Calcola il modulo di tutte le forze disegnate.
Svolgimento
Calcoliamo prima la forza peso, cioè la forza verso i basso
= m •g = 3,5 kg • 9,8 N/kg = 34,3 N verso il basso
E poi la forza di tensione cioè la forza vincolare che si oppone alla forza peso e che sostiene il lampadario e sarà verso l’alto.
sarà uguale al peso, con il verso contrario, se il lampadario è fermo in equilibrio
= 34,3 N forza verso l’alto.
ESERCIZIO N°2
Un appendiabiti è poggiato sul pavimento. In quel punto, il pavimento sviluppa una forza vincolare di 150 N.
Calcola la massa dell’appendiabiti.
Svolgimento
La forza vincolare sarà uguale alla forza peso.
= m • g
ESERCIZIO N°3
Una pallina di massa 250g è in equilibrio, appesa verticalmente a una molla fissata al soffitto. La molla è allungata di 4,2 cm rispetto alla sua lunghezza a riposo.
Disegna uno schema della situazione indicando le forze che agiscono sulla pallina.
Calcola il peso della pallina.
Individua il modulo della forza elastica esercitata dalla molla.
Determina il valore della costante elastica della molla.
Svolgimento
Sulla pallina agiscono più forze e cioè la forza elastica e la forza peso quindi la forza totale sarà:
= 0 sulla pallina agiranno la forza peso e la forza elastica, poichè la pallina è in equilibrio, la forza peso sarà uguale e opposta alla forza elastica. Le due forze si bilanciano e quindi si annullano
= m • g = 9,81 • 0,25 = 2,45 N ≅ 2,5 N
Portiamo i 4,2 cm a metri quindi 0,042 m
La forza elastica è sempre 2,5 N
quindi
ESERVIZIO N°4
Una molla, disposta in orizzontale, ha un estremo fissato al muro e l’altra estremità legata a un mattone che pesa 27 N. La costante elastica della molla è k = 180 N/m e il coefficiente di attrito statico tra il mattone e il pavimento vale 0,90. Con la mano afferri il mattone e lo fai strisciare sul pavimento fino ad allungare la molla di 20 cm.
Qual è il modulo della forza elastica e della forza al distacco tra mattone e pavimento?
Se lasci andare il mattone, questo si mette in moto?
Svolgimento
Sul corpo agiscono due forze : la forza elastica e la forza di attrito tra il mattone e il pavimento
Con i dati ci possiamo facilmente ricavare entrambe le forze :
Prima di calcolare la forza elastica convertiamo i 20 cm il 0,20 m
La forza elastica è maggiore della forza di distacco cioè la forza di attrito quindi quando rilasceremo il mattone esso si muoverà verso il muro.
ESERCIZIO N°5
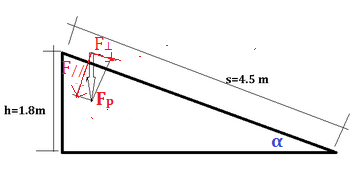
Uno scivolo di un parco giochi è alto 1,8 m e lungo 4,5 m.
Su di esso si trova un bimbo che ha massa 28 kg.
Con quale forza si deve afferrare al bordo dello scivolo per rimanere fermo?
Svolgimento
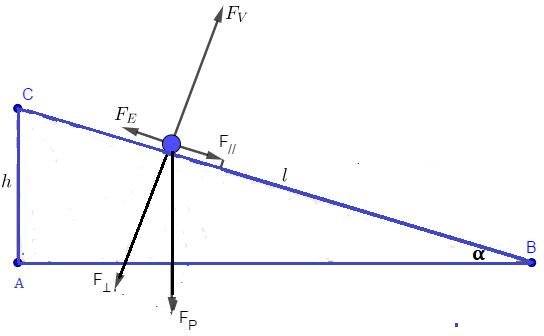
Possiamo considerare il bambino come se stesse su di un piano inclinato dove la forza peso si scopone nelle sue componenti e cioè la forza perpendicolare e la forza parallela, quest’ultima sarà quella che farà scende il bambino lungo lo scivolo. Il bambino per stare fermo deve contrastare solo la forza parallela poichè la forza perpendicolare è bilanciata dalla forza vincolare che è perpendicolare ma rivolta verso l’alto.
Vediamo per capire meglio con un disegno come come si dividono le forze:
Forza parallela al piano che fa scivolare la bambina:
F// =
sen α = 0,4
F// = 0,4 • 275 N ≅ 110 N
Per rimanere ferma occorre una forza contraria alla forza parallela agente verso il basso pari a : F = 110 N.
ESERCIZIO N°6
Un vaso di fiori di massa 15 kg viene appoggiato su una pedana di lunghezza 10 m e altezza 1,5 m. Il vaso è in equilibrio.
Quanto vale la forza equilibrante?
Svolgimento
Prima di tutto ci calcoliamo la forza peso:
F// = = 0,15 • 147 N ≅ 22 N
ESERCIZIO N°7
Per tenere in equilibrio un carrello della spesa su un piano inclinato lungo 4,00 m e alto 0,75 m è necessaria una forza di 92 N.
Qual è la massa del carrello?
Svolgimento
F// = = sen α • mg da qui ci esplicitiamo la massa quindi:
ESERCIZIO N°8
Un’automobile è parcheggiata su una strada in discesa, con il freno a mano tirato. La pendenza della strada è del 10% (la strada sale di 10 m per 100 m di spostamento orizzontale). La massa dell’automobile è di 840 kg.
Qual è il valore della forza di attrito che tiene ferma l’automobile agendo sugli pneumatici?
Svolgimento
La forza di attrito dovrà bilanciare la forza parallela per fare in modo che l’auto sia in equilibrio .
A questo punto ci serve l’angolo d’inclinazione della strada.
h corrisponde al 10% quindi 10 su 100 e la lunghezza= 100
Ora possiamo calcolare la forza parallela che è uguale alla forza equilibrante.
ESERCIZIO N°9
La rampa di carico di un magazzino è inclinata di 20°. Su di essa è fermo un carrello di massa 130 kg.
Rappresenta in un disegno le forze che agiscono sul carrello.
Calcola l’intensità della reazione vincolare della rampa. [1,2 x 103 N]
Svolgimento

F// = m•g•sin 20° essa è la forza che tende a far scivolare il carrello lungo il piano inclinato
La forza equilibrante è uguale e contraria ad F// e che mantiene il carrello fermo
è la componente della perpendicolare al piano inclinato ed è bilanciata dalla forza vincolare del piano inclinato
Fv = m•g•cos 20° = 130•9,8•0,940 = 1198 N cioè 1,2 • N
ESERCIZIO N°10
Un uomo e un bambino spingono un divano come nel disegno. La forza esercitata dall’uomo ha un’intensità doppia rispetto a quella esercitata dal bambino. I valori delle forze sono = 200 N e
= 100 N. Inoltre, la distanza fra il punto di applicazione della risultante e quello della forza
è
= 0,60 m.
Determina graficamente il punto di applicazione della forza risultante e l’intensità di tale forza.
A quale distanza dalla forza risulta applicata la forza risultante?
Svolgimento
ESERCIZIO N°11
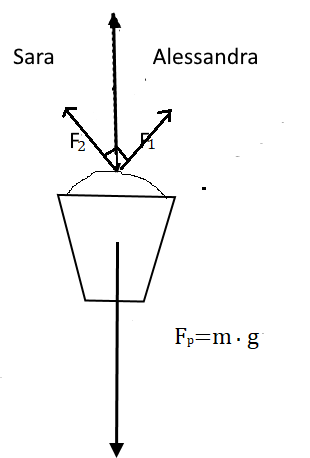
Sara e Anna vogliono tirar fuori un secchio di massa 15 kg da un pozzo poco profondo. Al manico del secchio sono legate due funi e ognuna delle due ragazze ne tiene in mano un capo. Tirano le funi con una forza di 57 N ciascuna e le funi formano con la verticale un angolo di 45°
Rappresenta con un disegno la situazione. Come sono le forze tra loro?
Complessivamente che forza esercitano Sara e Anna sul secchio?
Riescono a estrarlo?
Svolgimento
Sul secchio agiscono la forza peso e le forze di Sara ed Alessandra. La prima tende a far andare giù l secchio, le altre due a far salire il secchio.
Poichè l’angolo che formano con la verticale è di 45°, significa che l’angolo tra le due forze è di 90° , quindi sono perpendicolari tra loro
= m • g = 15 • 9,8 = 147 N diretta verso il basso;
Il modulo della forza risultante è dato dal teorema di Pitagora:
quindi Sara e Alessandra non riescono a sollevare il secchio.
Ci vuole una forza uguale o superiore a 147 N.
ESERCIZIO N°12
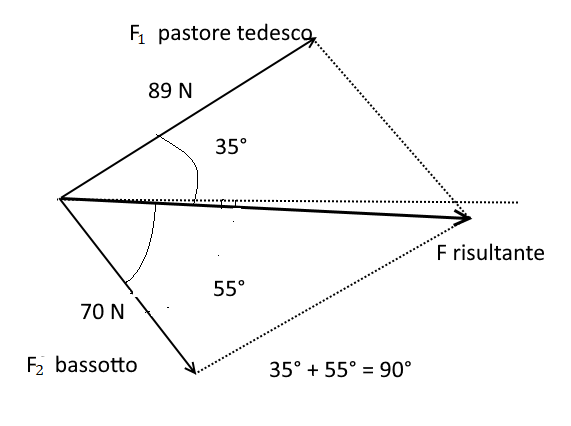
Federica passeggia con i suoi due cani al parco. Il pastore tedesco tende la corda del guinzaglio con una forza di 89 N mentre il bassotto esercita una forza di 70 N. Le corde dei guinzagli formano con la direzione in cui Federica sta camminando rispettivamente un angolo di 35° e uno di 55°.
Rappresenta con un disegno la situazione.
Trova l’intensità della forza risultante.
Svolgimento
35° + 55° = 90° quindi fra le due corde in tensione c’è un angolo retto.
La forza risultante è la diagonale del rettangolo che ha per lati i due vettori forza.
ESERCIZIO N°13
Un’asta lunga 120 cm è fatta ruotare intorno a uno dei suoi estremi per mezzo di una forza di intensità pari a 25 N, applicata all’altro estremo e perpendicolare all’asta.
Quanto vale il momento della forza rispetto al punto intorno al quale avviene la rotazione?
Svolgimento
Il momento di una forza è definito come:
Essendo il vettore r e il vettore F tra loro perpendicolari, risulta
sin(90°) = 1 quindi il modulo del momento è :
M= F x r
M= 1,20 • 25 = 30 N•m
ESERCIZIO N°14
Agli estremi di una sbarra sono applicate due forze uguali e opposte, di intensità pari a 65 N. Il momento della coppia vale 50 N•m.
Quanto è lunga la sbarra?
Svolgimento
Il momento di una coppia di forze si calcola sommando i momenti delle forze rispetto al punto medio rispetto ai loro punti di applicazione e sarà uguale al prodotto tra il modulo delle forze e la distanza tra le rette d’azione delle due forze.
ESERCIZIO N°15
Una coppia di forze, ognuna di valore 50,0 N, è applicata agli estremi di un’asta lunga 80,0 cm, vincolata nel centro, come nella figura.
Calcola il momento della coppia.
Qual è il verso di rotazione dell’asta?
Svolgimento
Nel momento di una coppia di forze, come in figura, il braccio diventa la lunghezza totale dell’asta, quindi:
braccio = 80 cm = 0, 8 m
il momento della coppia di forze M = F • b • sin α= 50 • 0,8 • sin (60°)= 34,6 N •m
Oppure possiamo ragionare così:
Per calcolare il momento della coppia di forze, calcoliamo ogni singolo momento e poi li sommiamo, facendo attenzione al verso. In questo caso sono concordi . Inoltre hanno anche uguale modulo perchè le forze hanno lo stesso modulo e l’angolo è lo stesso.
Quindi Momento= 2 •M= 2 • F • b • sin α = 2 • 50 N • 0,4 m = 34,6 N • m
ESERCIZIO N°16
Su una tavoletta quadrata di lato 3,0 cm vengono applicate quattro forze con la stessa intensità pari a 10 N come nella figura.
* Calcola il modulo del momento risultante rispetto al centro del quadrato. Suggerimento: scomponi le forze nelle direzioni parallele alle diagonali del quadrato.
Svolgimento
Per calcolare il momento di più forze si può calcolare il momento di ogni singola forza e sommarli. La forza ,
,
hanno un momento concorde,
discorde.
Quindi il momento totale sarà:
è nullo perchè il braccio e la forza coincidono, infatti il braccio è dato dal prolungamento della forza con il centro.
Il braccio del secondo momento è la metà del lato.
l’angolo è retto perchè forza e braccio sono perpendicolari.
Il calcolo del terzo braccio è semplice poichè è la metà della diagonale del quadrato quindi poichè la diagonale di un quadrato è lato • , quindi metà diagonale è pari a (3 •
) : 2 = 2,12 cm quindi 0,02 m.
ESERCIZIO N°17
Lorenzo cerca di aprire una porta e Giovanni tenta di impedirglielo. Entrambi esercitano una forza perpendicolare alla porta. Lorenzo esercita una forza di 151 N applicata a 70 cm dai cardini mentre Giovanni esercita una forza di 200 N applicata a 50 cm dai cardini.
Calcola il modulo del momento complessivo delle forze rispetto ai cardini della porta.
La porta si apre o rimane chiusa?
Svolgimento
Per calcolare il modulo del momento complessivo basta sommare i singoli momenti che in questo caso sono opposti quindi uno positivo e l’altro negativo.
Il valore trovato è positivo quindi il momento applicato da Lorenzo è maggiore di quello di Giovanni quindi la porta si apre.
ESERCIZIO N°18
Uno svitatappi con il manico di 17 cm viene utilizzato per aprire un barattolo. Il tappo si svita se viene applicata una forza di 120 N. Luca riesce ad applicare al massimo una forza inferiore di un terzo.
Calcola il modulo del momento della forza necessario per svitare il tappo.
Quanto dovrebbe essere lungo il manico dello svitatappi adatto a Luca?
Svolgimento
17 cm = 0,17 m
Il modulo del momento necessario a svitare il tappo è:
M= F • b = 120 N• 0,17 m= 20,4 N • m
Se luca riesce ad imprimere una forza di 80 N e il momento necessario per aprire il tappo è 20,4 N • m , applichiamo la formula inversa . Quindi:
cioè 26 cm
ESERCIZIO N°19
Una bambina di massa 22 kg è seduta su un’altalena. Il papà porta indietro il sellino finchè la corda tesa non forma con la verticale un angolo di 60°, poi lo lascia andare.
La corda dell’altalena misura 2,1 m.
Calcola il momento della forza-peso della bambina rispetto al punto di aggancio della corda nel momento in cui il sellino viene liberato dalla presa.
Svolgimento
Il braccio dal punto di applicazione della forza al punto rispetto al quale va calcolato il momento è lungo 2,1 m mentre il modulo è quello della forza peso cioè m •g. Il modulo del momento della forza vale sin (90°) = 393 N • m cioè 3,9 • 10²
ESERCIZIO N°20
Un ragazzo sta giocando con un aquilone. Il rocchetto dell’aquilone è un’assicella con il filo avvolto al centro come nella figura. Il rocchetto viene impugnato con le mani alle estremità dell’assicella. Il vento mette in tensione il filo con una forza di 58 N.
Quali forze deve applicare il ragazzo perché il rocchetto sia in equilibrio?
Svolgimento
Poiché il rocchetto viene impugnato con le mani alle estremità dell’assicella, la forza del vento viene divisa in due parti uguali. Quindi 58 N : 2 = 29 N
Ovviamente la forza esercitata da ciascuna mano è 29 N.
ESERCIZIO N°21
Un quadro è appeso a una parete con due fili come nella figura. La tensione dei fili è uguale e vale 13 N. Il quadro si trova in equilibrio.
Calcola la massa del quadro.
Verifica che il momento delle forze rispetto al punto O è nullo.
Svolgimento
La somma delle forze agenti sul corpo è pari a zero
La somma dei momenti è zero
Le due tensioni hanno stessa direzione ma verso opposto alla forza peso.
Calcoliamo la massa del quadro
2•T = P = m•g
Il momento delle forze calcolato rispetto al punto O è nullo perché le due forze generano momenti aventi stesso modulo e direzione ma verso opposto.
Stesso modulo perché:
M= F•b dove:
F= modulo della forza
b= braccio = distanza del punto O dalla retta d’azione delle due forze.
Nel nostro problema ||=|
| e
=
⇒ |
|=|
|
ESERCIZIO N°22
Una bilancia a bracci disuguali, uno di 38 cm e l’altro di 23 cm, è in equilibrio. Sul piatto appeso al braccio più lungo è appoggiata una bottiglia d’acqua da 1,0 L. Sull’altro piatto c’è un libro.
Quanto pesa il libro?
Quanto vale il modulo della reazione vincolare sul perno della bilancia?
Svolgimento
Per svolgere il problema si eguagliano i due momenti.
M = b • F
poichè la forza peso è uguale a m • g riscriviamo l’uguaglianza
Per avere l’equilibrio, sul fulcro deve agire una forza verso l’alto uguale alla somma delle forze agenti verso il basso.
Quindi la forza peso totale è data dalla somma delle singole forze peso
ESERCIZIO N°23
Pare che Archimede da Siracusa abbia detto: «Datemi una leva e vi solleverò il mondo».
Quanto dovrebbe essere lunga una leva di primo genere per equilibrare l’attrazione gravitazionale che il Sole esercita sulla Terra con una forza di 150 N? Ti serve sapere che la forza d’attrazione gravitazionale è dell’ordine di 102 N e puoi immaginare un braccio della forza resistente dell’ordine della decina di kilometri.
Svolgimento
150 N = 1,5 • N
ESERCIZIO N°24
Un bambino è seduto a uno dei due estremi di un’altalena a 2,12 m dal fulcro centrale. Il padre lo fa giocare premendo l’altro braccio dell’altalena a 1,56 m dal centro. Il peso del bambino è pari a 170 N.
Quale forza deve esercitare il padre, in direzione perpendicolare all’altalena, per fare in modo che questa rimanga in posizione orizzontale e non ruoti?
Svolgimento
Calcoliamo prima di tutto il momento generato dal peso del bambino rispetto al fulcro centrale dell’altalena.
M = b • F
= 2,12 m • 170 N = 360 N· m
Ora calcoliamo il momento generato dalla forza esercitata dal padre rispetto al fulcro centrale dell’altalena.
= F • 1,56 m
Poichè per mantenere l’altalena in posizione orizzontale e in equilibrio, i due momenti devono essere uguali, allora li eguagliamo:
360 N· m= F • 1,56 m
ESERCIZIO N°25
In una leva di primo genere, i bracci della forza motrice e della forza resistente sono rispettivamente di 2,50 m e 0,80 m. La forza motrice ha un’intensità di 15 N.
Quale forza resistente è possibile equilibrare con questa leva?
Svolgimento
M = F • b
ESERCIZIO N°26
In una leva di terzo genere i due bracci misurano 80 mm e 55 mm. La leva è in equilibrio sotto l’azione di una forza resistente di 5,7 N.
Qual è l’intensità della forza motrice?
Svolgimento
E’ una leva di terzo genere e quindi la forza motrice è tra fulcro e la forza resistente.
Il braccio motore è più corto di quello resistente. Quindi il braccio motore è 55 mm e il resistente 80 mm
55mm = 0,055 m
80 mm = 0,,80 m
ESERCIZIO N°27
Nella figura è rappresentata una leva sottoposta all’azione di una forza resistente di 12N.
Quanto vale l’intensità della forza motrice in grado di equilibrare la forza resistente?
Di che genere è la leva?
È vantaggiosa o svantaggiosa?
Svolgimento
Il braccio motore sarà uguale a 38 + 12 = 40 cm
Il braccio resistente 8 cm
E’ una leva di secondo genere vantaggiosa.
ESERCIZIO N°28
Un’asse di legno lunga 2,3 m è utilizzata per sollevare un grosso macigno di massa 100 kg. A un’estremità viene applicata una forza motrice di 195 N.
A che distanza dal macigno è posizionato il fulcro della leva?
Svolgimento
Partiamo con il dire che il braccio motore più il braccio resistente sono uguali a 2,3 m
Svolgo l’equazione
porto gli unici dati ce non conosco a destra
ESERCIZIO N°29
Roberto sta pulendo il pavimento con una scopa lunga 1,50 m. Impugna la scopa con entrambe la mani, la sinistra all’estremità e la destra 30 cm più in basso. Sul pavimento c’è un secchio di massa 5,0 kg e Roberto lo sposta con la scopa muovendo la mano destra. Il coefficiente d’attrito tra il secchio e il pavimento è 0,60.
Che genere di leva è la scopa?
Che forza ha esercitato Roberto con la mano destra per spostare il secchio?
Svolgimento
La forza resistente è la forza di attrito che ci calcoliamo
Il braccio della forza resistente è la lunghezza della scopa, il braccio della forza motrice è 30 cm cioè 0,3 m
E’ una leva svantaggiosa perchè il braccio della resistenza è più lungo del braccio motore
ESERCIZIO N°30
ll meccanismo della serranda del negozio di un tuo amico si è rotto e lui è rimasto chiuso fuori. Devi sollevarla di almeno 35 cm per permettergli di entrare. La serranda ha una massa di 230 kg. Hai a disposizione una leva lunga 2,30 m e la forza massima che puoi esercitare è 350 N.
A quale distanza dalla serranda devi posizionare il fulcro della leva?
Svolgimento
La forza resistente è data dal peso della serranda che ci andiamo a calcolare.
0,3 m = 30 cm
ESERCIZIO N°31
L’apribottiglie della figura è utilizzato per togliere un tappo a corona, che oppone una forza resistente di 120 N. II braccio della resistenza è lungo 1,2 cm, quello della forza motrice 7,2 cm.
Di che tipo di leva si tratta?
Quale forza motrice serve per equilibrare la forza resistente?
Che cosa succede se applichiamo una forza motrice maggiore di quella appena calcolata?
Svolgimento
le leve di primo genere sono le leve in cui il fulcro è compreso tra i punti dove vengono applicate la forza motrice e la forza resistente. Esempi: le forbici
le leve di secondo genere sono le leve in cui la forza resistente agisce tra la forza motrice e il fulcro. Esempi: la carriola e lo schiaccianoci
le leve di terzo genere sono le leve in cui la forza motrice agisce tra la forza resistente e il fulcro. Esempi: il bicipite umano o una pinzetta.
E’ una leva di primo genere vantaggiosa
Se applichiamo una forza motrice maggiore acceleriamo la manovra.