Esercizio sul peso specifico
Problema n° 1
Dato un solido di peso P e volume V, formato da una sostanza di peso specifico :
a) se P = 40,5 kg e Ps = 2,7
b) se V = 20 cm³ e Ps = 0,55
c) se P = 234 g e V = 12 cm³
Problema n° 2
L’oro e l’argento hanno rispettivamente peso specifico 19,5 e 10,5. Se un oggetto d’oro massiccio pesa 546 g, quanto peserebbe se fosse d’argento?
Problema n° 3
Un oggetto cavo viene riempito con 450 g di sabbia. Sapendo che il peso specifico della sabbia è 1,5 qual è il volume dell’oggetto?
Problema n° 4
In un cilindro graduato contenente 200 cl d’acqua, viene immerso un oggetto di piombo (Ps piombo = 11,3) e il livello dell’acqua si porta a 250 cl. Qual è il peso dell’oggetto?
Problema n° 5
Un oggetto pesa 1,5 kg. Immerso in un cilindro graduato contenente 5 dl di acqua, fa salire il livello a 11 dl. Qual è mil peso specifico dell’ oggetto?
Problema n° 6
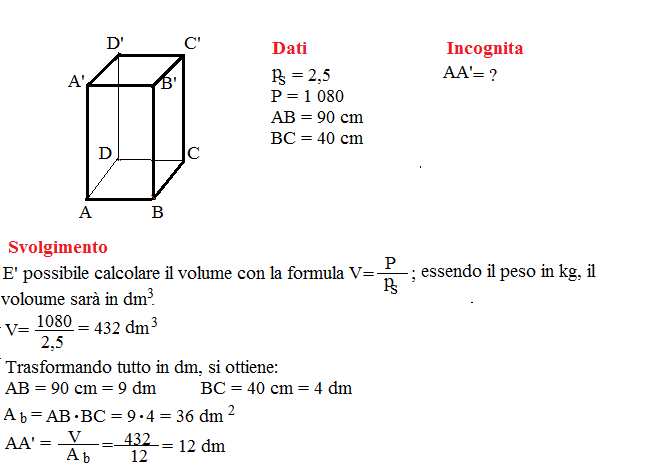
Un solido di vetro (Ps = 2,5) pesa 1 080 kg. Sapendo che ha la forma di un parallelepipedo rettangolo con le dimensioni di base lunghe rispettivamente 90 cm e 40 cm, calcola la misura della sua altezza.
Problema n° 7
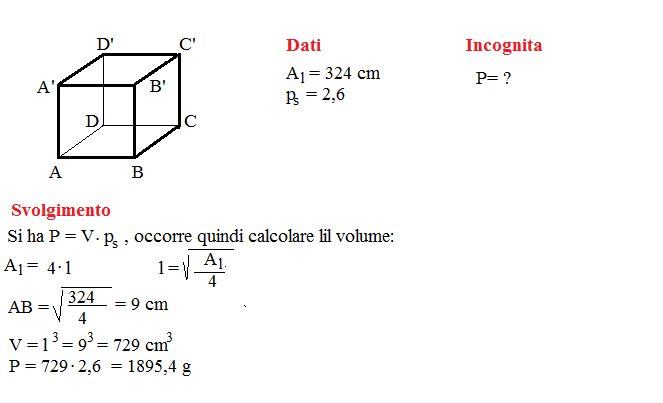
L’area laterale di un cubo è 324 cm². Calcola il peso del solido sapendo che è fatto di marmo (Ps = 2,6).
Problema n° 8
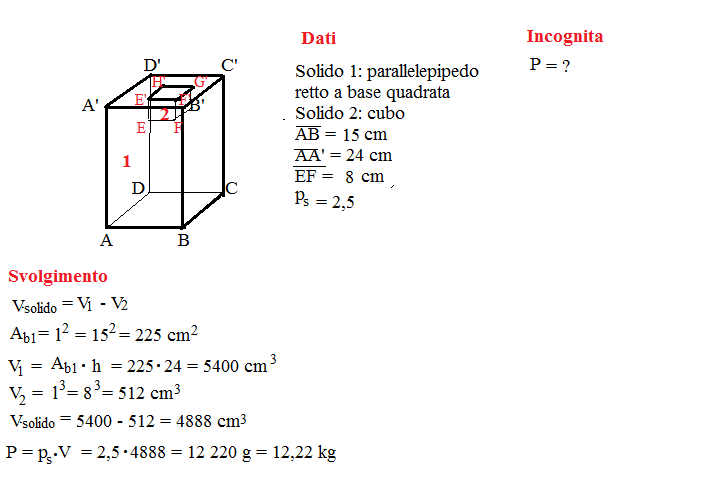
Un oggetto di vetro (Ps = 2,5) è formato da un parallelepipedo retto a base quadrata in cui è stata praticata una cavità cubica con lo spigolo di 8 cm. Sapendo che lo spigolo di base e l’altezza del parallelepipedo sono lunghi rispettivamente 15 cm e 24 cm, calcola il peso dell’oggetto.
Problema n° 9
Una colonna di marmo è alta 3 m e ha la forma di un cilindro. Sapendo che la circonferenza di base misura 314 cm e che il peso specifico del marmo è 2,5, calcola il peso della colonna.
SVOLGIMENTO
Problema n° 1
Dato un solido di peso P e volume V, formato da una sostanza di peso specifico Ps:
a) se P = 40,5 kg e Ps = 2,7
b) se V = 20 cm³ e Ps = 0,55
P = (20 x 0,55) g = 11 g
c) se P = 234 g e V = 12 cm³
Problema n° 2
L’oro e l’argento hanno rispettivamente peso specifico 19,5 e 10,5. Se un oggetto d’oro massiccio pesa 546 g, quanto peserebbe se fosse d’argento?
Svolgimento
Dobbiamo prima trovare il volume dell’oro:
A questo punto possiamo trovare il peso dell’oggetto se fosse d’oro:
Problema n° 3
Un oggetto cavo viene riempito con 450 g di sabbia. Sapendo che il peso specifico della sabbia è 1,5 qual è il volume dell’oggetto?
Svolgimento
Problema n° 4
In un cilindro graduato contenente 200 cl d’acqua, viene immerso un oggetto di piombo (Ps piombo = 11,3) e il livello dell’acqua si porta a 250 cl. Qual è il peso dell’oggetto?
Svolgimento
Il volume dell’oggetto è dato dalla quantità di liquido spostato, quindi:
V = (250 – 200) = 50 cl
Poichè la capacità di 1 l equivale al volume di 1 dm³, si ha:
V = 50 cl = 0,5 l = 0,5 dm ³
P = V x Ps P = 0,5 x 11,3 = 5,65 kg
Problema n° 5
Un oggetto pesa 1,5 kg. Immerso in un cilindro graduato contenente 5 dl di acqua, fa salire il livello a 11 dl. Qual è il peso specifico dell’ oggetto?
Svolgimento
Il volume dell’oggetto sarà uguale alla differenza dei due volumi che rappresentano la quantità di liquido spostato.
V = 11-5 = 6 dl = 0,6 l = 0,6 dm ³
1,5 kg = 1500 g
Problema n° 6
Un solido di vetro (Ps = 2,5) pesa 1 080 kg. Sapendo che ha la forma di un parallelepipedo rettangolo con le dimensioni di base lunghe rispettivamente 90 cm e 40 cm, calcola la misura della sua altezza.
Problema n° 7
L’area laterale di un cubo è 324 cm². Calcola il peso del solido sapendo che è fatto di marmo (Ps = 2,6).
Problema n° 8
Un oggetto di vetro (Ps = 2,5) è formato da un parallelepipedo retto a base quadrata in cui è stata praticata una cavità cubica con lo spigolo di 8 cm. Sapendo che lo spigolo di base e l’altezza del parallelepipedo sono lunghi rispettivasmente 15 cm e 24 cm, calcola il peso dell’oggetto.
Problema n° 9
Una colonna di marmo è alta 3 m e ha la forma di un cilindro. Sapendo che la circonferenza di base misura 314 cm e che il peso specifico del marmo è 2,5, calcola il peso della colonna.
