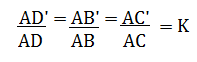Consideriamo queste due figure:
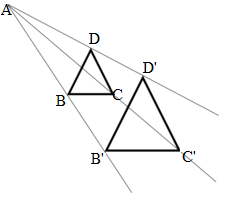
I triangoli BCD e B’C’D’ sono simili, ma oltre a essere simili hanno un ‘ altra caratteristica in più e cioè i lati corrispondenti hanno la stessa direzione cioè sono paralleli.
Nel linguaggio matematico si dice che le due figure sono omotetiche.
La trasformazione che lega le due figure è detta omotetia.
Possiamo verificare usando un righello, che le rette passanti per i punti corrispondenti, cioè le rette DD’, CC’, BB’ si incontrano tutte in uno stesso punto A, detto centro di omotetia.
Due figure sono omotetiche se i loro punti corrispondenti sono allineati su rette che si incontrano tutte in un punto, detto centro dell’omotetia, e i loro lati corrispondenti sono in rapporto costante. Tale rapporto di proporzionalità k, si chiama rapporto di omotetia.
Nel caso dei triangoli della figura di sopra avremo:
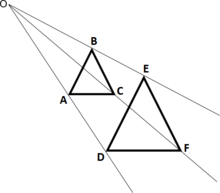
Per costruire due figure omotetiche F ed F’ occorre conoscere il centro di omotetia e il rapporto di omotetia k.
La caratteristica k dell’omotetia determina il rimpicciolimento o l’ingrandimento della figura. In particolare:
• Se k > 1 si ha un ingrandimento della figura trasformata rispetto ad una figura presa in esame, questo avviene sia nella omotetia diretta che in quella inversa;
• Se k < 1 si ha un rimpicciolimento della figura trasformata rispetto ad una figura presa in esame, questo avviene sia nella omotetia diretta che in quella inversa;
• Per k = 1 la figura trasformata rispetto ad una figura presa in esame è coincidente se l’omotetia è diretta, si dice quindi che è un’identità. Nell’omotetia inversa si ha una simmetria centrale.
Un’omotetia può essere diretta o inversa.
• Parliamo di omotetia diretta se i vertici corrispondenti si prendono, rispetto al centro dell’omotetia, dalla stessa parte dei vertici della figura data. Quindi la figura e la sua immagine sono dalla stessa parte rispetto al centro di omotetia.
- Parliamo di omotetia inversa se i vertici corrispondenti si prendono, rispetto al centro dell’omotetia, dalla parte opposta dei vertici della figura data. Quindi la figura e la sua immagine sono da parti opposte rispetto al centro di omotetia.