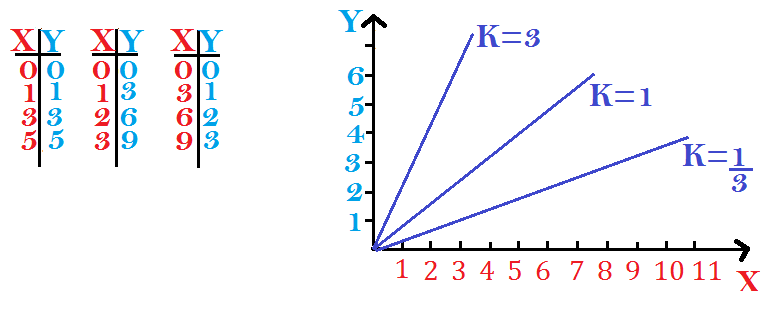
Rappresentazione della legge della proporzionalità diretta
La rappresentazione grafica di y=k·x è una retta passante passante per l’origine.
Per la proprietà della moltiplicazione e della divisione, la relazione y=k·x può essere anche scritta come y\x=k oppure x=y\k
Tale retta y=k·x varia la sua posizione nel piano cartesiano al variare del valore k.
per k=1 , y=x per k=3 , y=3x per k=1\3, y=1\3x
Per disegnarla si da un valore alla x e si vede la y quanto vale:
Due grandezze variabili sono inversamente proporzionali se raddoppiando, triplicando la variabile indipendente x, la variabile dipendente y si dimezza e diventa un terzo; analogamente se la prima si dimezza o diventa un terzo, la seconda diventa il doppio, il triplo.
Analogamente:
Due grandezze x e y sono inversamente proporzionali se il prodotto di due valori corrispondenti si mantiene costante.
y·x=k con k>0;
k è il coefficiente di proporzionalità inversa y =k\x è detta equazione della proporzionalità inversa.