SOTTOINSIEMI
Si definisce B sottoinsieme di A se ogni elemento di B appartiene anche ad A, ma c’è almeno un elemento di A che non è presente in B.
Per esempio:
A={X/X vocale dell’alfabeto italiano } B={x/x vocale della parola mare };
A={a,e,i,o,u}; B={a,e};
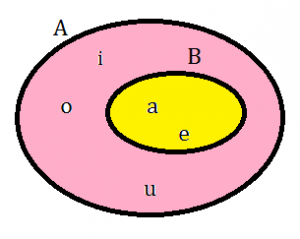
In questo caso tutti gli elementi di B appartengono ad A quindi B è un sottoinsieme. Si dice che B⊂A e si legge l’insieme B è contenuto o incluso in A.
Per dire che A non è contenuto in B si scriverà A⊄B
Ogni insieme ammette due sottoinsiemi detti impropri e cioè l’insieme vuoto e se stesso.
Gli insiemi uguali
Due insiemi sono uguali se sono formati dagli stessi elementi.
A= {a, e, i, o, u}
B= {x/x vocale della parola “aiuola” }
sono insiemi uguali, perchè hanno gli stessi elementi.
Per stabilire che A=B, basta controllare che sie:
A⊆B e B⊆A
Infatti, se A⊆B tutti gli elementi di A sono elementi di B, e se B⊆A, anche tutti gli elementi di B sono elementi di A, perciò A e B hanno gli stessi elementi.
Per esempio consideriamo l’insieme A dei multipli di 2 minori di 10 e l’insieme B dei numeri pari minori di 10.
Ogni multiplo di 2 è anche numero pari, quindi:
A⊆B;
ogni numero pari è multiplo di 2, quindi:
B⊆A
Pertanto A=B.
E’ vero anche il viceversa, cioè se A=B allora A⊆B e B⊆A
L’inclusione stretta
Si dice che l’insieme B è strettamente incluso nell’insieme A quando ogni elemento di B è anche elemento di A, ma esistono elementi di A che non sono elementi di B.
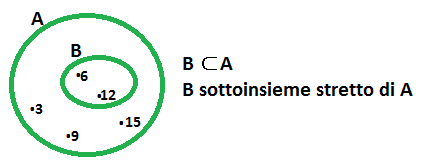
Si scrive B ⊂ A e si legge “B è un sottoinsieme stretto di A”, oppure ” B è incluso strettamente in A”.
P ⊂ N, perchè tutti i numeri pari sono naturali, ma esistono naturali che non sono pari.
I sottoinsiemi propri e impropri
Per qualunque insieme A vale la relazione:
∅ ⊆ A .
Infatti, poichè l’insieme vuoto non ha elementi, possiamo sempre affermare che ogni elemento dell’insieme vuoto è anche elemento dell’insieme A.
Pertanto, dato un insieme, l’insieme stesso e l’insieme vuoto sono chiamati sottoinsiemi impropri.
Ogni sottoinsieme non vuoto strettamente incluso in un insieme si dice sottoinsieme proprio dell’insieme.
Per esempio:
- L’insieme A delle consonanti della parola “aia” è un sottoinsieme improprio dell’insieme delle consonanti, perchè A= ∅.
- L’insieme B delle vocali della parola ” aiuole” è un sottoinsieme improprio dell’insieme V delle vocali, perchè B=V.
- L’insieme I delle lettere dell’alfabeto italiano è un sottoinsieme proprio dell’insieme E delle lettere dell’alfabeto inglese, perchè I non è vuoto; ogni elemento di I è elemento di E, ma esistono elementi di E (per esempio la lettera w) che non sono elementi di I.