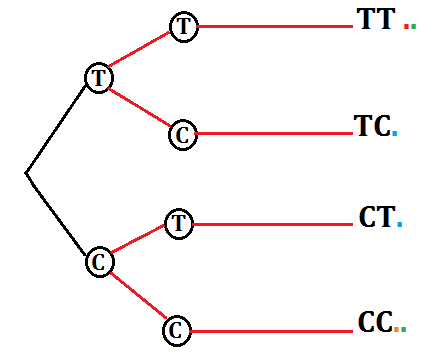
Consideriamo il lancio di due monete che da una faccia hanno testa e dall’altra croce e rappresentiamo il così detto GRAFO AD ALBERO
Casi possibili (TT),(TC),(CT),(CC).
CALCOLARE LA PROBABILITA’ DI EVENTI
La probabilità di “avere due teste” è la probabilità di avere l’evento A={T,T} quindi p(A)=1\4.
Osserviamo anche che 1 è il numero degli elementi di A e 4 è il numero di elementi dello spazio campionario.
Allo stesso tempo la probabilità di “avere due croci “,cioè dell’evento B={C,C} corrisponde nel grafo ad albero ad un unico esito favorevole(indicato dal pallino giallo) p(B)=1\4.
La probabilità di “ottenere facce diverse” è la probabilità dell’evento D= {(T,C);(C,T)}. Ci sono quindi due elementi nel grafo ad albero favorevoli a questo esito. Quindi p(D)=2\4=1\2.
Osserviamo che due sono gli elementi di A e 4 è il numero degli elementi dello spazio campionario.
Descriviamo infine l’evento E=” ottenere due facce uguali tra loro” e calcoliamo la sua probabilità.
I casi favorevoli nel grafo corrispondono ai pallini verdi e sono due:
E={(T,T),(C,C)} P(E)=2\4=1\2.
PROBLEMI E APPLICAZIONI
PROBLEMA 1
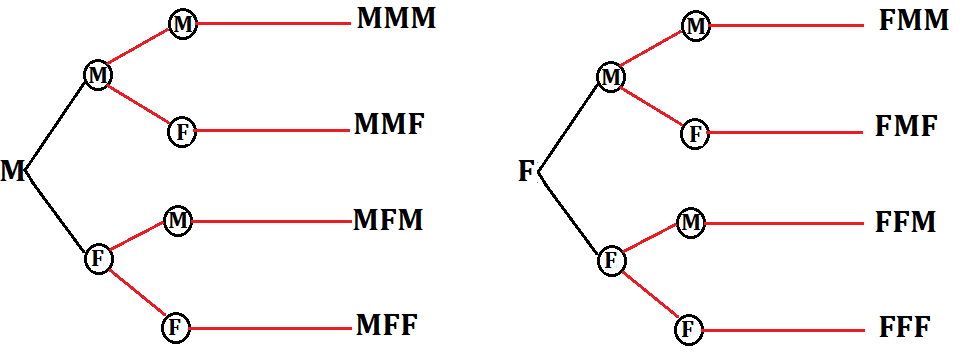
In una famiglia con tre figli, qual è la probabilità che siano tutti e tre femmine?
Schematizziamo il tutto in un grafo ad albero:
I casi ugualmente possibili 2·2·2=8
Si considera dal grafo il
PROBLEMA 2
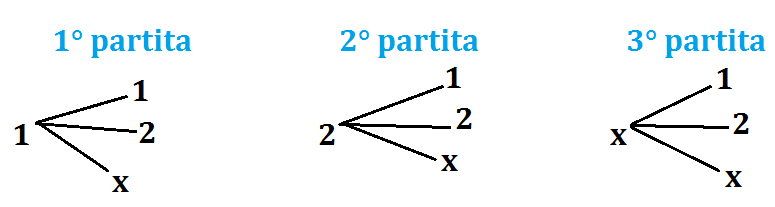
Se volessimo fare 13 sicuri quante colonne dovremmo giocare?
Supponiamo che ci siano solo 4 squadre e quindi che si giochino due partite e i risultati possibili sono 1,x,2:
Per due partite otteniamo ben 3•3= 9 casi possibili. Se le squadre fossero 6 otterremo 3•3•3= 27 casi possibili. Quindi avremo che per 8 squadre quindi 4 partite i casi possibili saranno