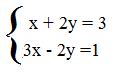Il metodo della riduzione anch’esso come il metodo del confronto, il metodo della sostituzione si applica una volta aver ridotto il sistema in forma normale. Questo metodo è anche detto metodo della combinazione lineare. Esso consiste nel rendere uguali oppure opposti i coefficienti di una delle due incognite e quindi moltiplicare ogni equazione per un numero o un certo segno, applicando il secondo principio di equivalenza, affinchè si raggiunga tale obiettivo. Alla fine si sottraggono o addizionano membro a membro, ottenendo così un’equazione ad una sola incognita. Si calcola il valore di questa incognita e lo si sostituisce ad una delle due equazioni iniziali, di solito è conveniente scegliere la più semplice, in modo da calcolare l’altra incognita.
Consideriamo un esempio per capire come procedere.
In questo caso possiamo notare che i coefficienti dell’incognita y sono già gli stessi, ma con segni opposti, quindi è un sistema in cui si può applicare il metodo della riduzione senza moltiplicare per alcun numero. Quindi direttamente possiamo addizionare le due equazioni membro a membro.
La soluzione del sistema è la coppia di numeri (1,1)
Facciamo ora un esempio più complesso, nel senso che ora dobbiamo scegliere di moltiplicare le equazioni per un numero in modo da ottenere almeno una incognita con lo stesso coefficiente.
La soluzione del sistema è la coppia di numeri (4\3; -1)