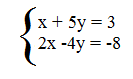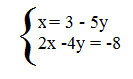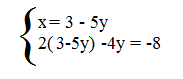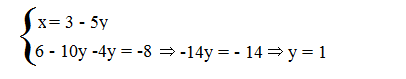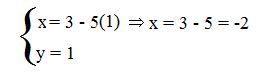Dopo aver ridotto il sistema in forma normale, il metodo della sostituzione consiste nell’esplicitare una delle due equazioni, quella che ci sembra più semplice , rispetto a una qualsiasi incognita. ad esempio x, e sostituire l’espressione trovata nell’altra equazione , al posto della x . Così si ottiene un’equazione nella sola incognita y, che si può risolvere : il valore della y ottenuto si sostituisce nell’espressione di x e si calcola anche il valore x.
Per esempio consideriamo il seguente sistema:
A questo punto si vede se le equazioni sono in forma normale, se non fosse così, le si portano in forma normale.
Si vede in quale delle equazioni è più semplice esplicitare la x o la y. Nel nostro caso sicuramente nella prima equazione.
A questo punto sostituiamo i valore della x della prima equazione nella seconda.
A questo punto la seconda equazione come incognita contiene solo le y . Ricaviamo il suo valore e la prima equazione rimane scritta sempre uguale.
Il valore della y verrà sostituito nella prima equazione e si otterrà un’equazione la cui unica incognita è la x; quindi si ricaverà il valore della x.
La soluzione del sistema è la coppia di numeri (-15 ; – 29).