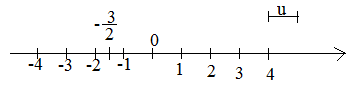Prima di parlare del piano cartesiano che usiamo in geometria analitica, consideriamo il caso più semplice e cioè quello in cui dobbiamo rappresentare un numero reale su di una retta.
Per fare ciò si traccia una retta orientata, si prende un punto qualunque e gli si attribuisce il valore 0, infine si stabilisce l’unità di misura e cioè quanto disterà un punto dall’altro.
Ovviamente i numeri positivi sono quelli che seguono lo 0 e cioè si trovano alla sua destra, invece i numeri negativi sono quelli che lo precedono e quindi sono alla sua sinistra.
A ogni punto della retta corrisponde uno e un solo numero reale e viceversa; quindi tra i punti della della retta e i numeri reali c’è una corrispondenza biunivoca.
Il numero reale che corrisponde a un punto P qualsiasi si dice ascissa del punto P sulla retta.
L’ascissa del punto rappresenta la distanza di P dall’origine 0.
Se invece di dover determinare il punto su di una retta lo dovessimo trovare su di un piano, bisogna introdurre il sistema di riferimento ortogonale.
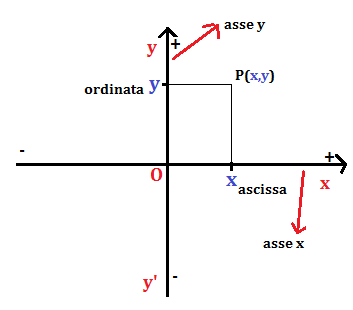
A questo punto devono essere considerate due rette orientate perpendicolari tra loro e verranno scelte una orizzontale e l’altra verticale. Il loro punto di incontro sarà chiamato O (origine degli assi).
Queste rette dividono il piano in quattro regioni che chiamiamo quadranti, di cui indichiamo con 1° quello in alto a destra e con 2°,3° e 4° gli altri, seguendo il verso antiorario.
L’asse orizzontale è detto asse dell’ascisse o asse delle x.
L‘asse verticale è detto asse delle ordinate o asse delle y.
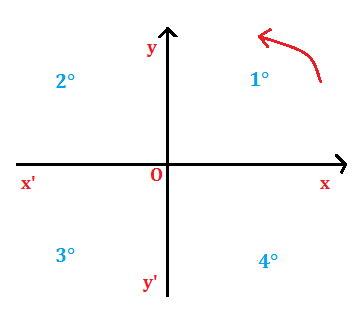
1° Quadrante: ascissa positiva; ordinata positiva.
2° Quadrante: ascissa negativa; ordinata positiva.
3° Quadrante: ascissa negativa; ordinata negativa.
4° Quadrante: ascissa positiva; ordinata negativa.
Se consideriamo un punto in tale piano cartesiano, formato dagli assi x e y che si incontrano nell’origine O, ogni punto P del piano è associato a una coppia ordinata di numeri relativi (x,y) cioè le sue coordinate cartesiane; l’ascissa x e l’ordinata y.
Ad ogni coppia ordinata di numeri reali corrisponde uno e un solo punto P nel piano o viceversa.
Il valore assoluto delle coordinate indica la distanza del punto dagli assi, il segno indica la posizione rispetto agli assi.
Il segno dell’ascissa x indica la posizione rispetto all’asse y; a destra (+) e a sinistra (-).
Il segno dell’ordinata y indica la posizione rispetto all’asse x sopra (+) e sotto(-)
E’ possibile stabilire una corrispondenza biunivoca tra i punti del pano cartesiano e le coppie ordinate di numeri relativi.
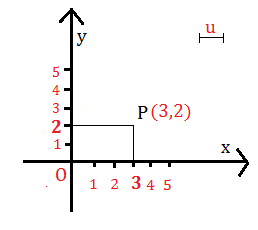
Se vogliamo determinare, sul piano, la posizione di un punto, rappresentato ad esempio, dalla coppia ordinata(+3,+2) dobbiamo tracciare due assi cartesiani perpendicolari x ed y che si incontrano nel punto O, fissare una unità di misura e determinare sull’asse delle x il punto A, tale che OA=3u e sull’asse y il punto B tale che sia OB= 2u e per i punti A e B condurre le perpendicolari agli assi. L’intersezione P è il punto richiesto.
I numeri +3 e +2 si dicono rispettivamente ascissa e ordinata del punto P ed entrambi si dicono coordinate di P
L’origine O degli assi ha l’ascissa 0 e l’ordinata 0. Esso si indica perciò con il simbolo O(0,0).
Esempio
Rappresenta i punti in un piano cartesiano.
A (+2 ; +4) , B (- 3 ; -5), C (+ 1; – 6) , D (- 4; + 2), E ( -4 ; 0), F (0; – 2)
Programma matematica secondo superiore
Programma matematica terzo superiore