Tale teorema afferma che: in un triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
Consideriamo due quadrati uguali e scomponiamo il primo nel quadrato A e nei triangoli rettangoli uguali 1,2,3,4, ed il secondo nei quadrati B e C e nei quattro triangoli rettangoli uguali ai precedenti, come indicato in figura.
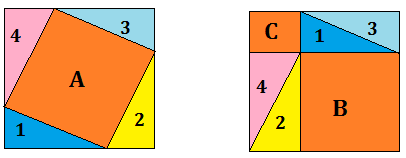
Se da entrambi i quadrati dati togliamo i quattro triangoli suddetti, rimangono, nella prima figura il quadrato A e nella seconda, i quadrati B e C.
Ricordando che se da figure uguali togliamo figure uguali rimangono figure equivalenti, abbiamo che:
Il quadrato A è equivalente alla somma dei quadrati B e C.
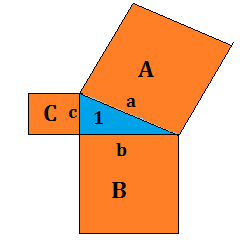
Osserviamo che il quadrato A è quello costruito sull’ipotenusa del triangolo rettangolo 1, mentre i quadrati B e C sono i quadrati costruiti sui cateti dello stesso triangolo 1. Quindi è dimostrato il teorema di Pitagora.