Un polinomio A(x) è divisibile per un binomio x-a se e soltanto A(a) è uguale a 0.
Se il polinomio A(x) = x³ + 2x² -13x + 10 è divisibile per x + 5, allora la divisione:
(x³ +2x² -13x +10):(x+5) dà resto 0; quindi, per il teorema del resto, A(-5)=0
Il ragionamento è invertibile.
Dato il polinomio A(x)=x³ +2x² -13x + 10, se A(-5)=0, allora la divisione: (x³ + 2x² -13x + 10) :(x + 5)
dà resto 0, per il teorema del resto; quindi x³ +2x² -13x + 10 è divisibile per x+5
Per esempio il polinomio A(x)=2x³ +x² -5x + 2 è divisibile sia per x-1 sia per x+2.
Andiamo a sostituire alla x prima 1 e poi -2:
A(1)=2 + 1 – 5 + 2 =0
A(-2)= 2(-8) + 4 – 5(-2) + 2 = -16 + 4 + 10 + 2= 0
Casi particolari
x³- a³ (differenza di cubi)
Consideriamo il binomio x³- a³ come polinomio A(x) e sostituiamo a x il valore a. Otteniamo:
A(a)= a³ – a³ =0
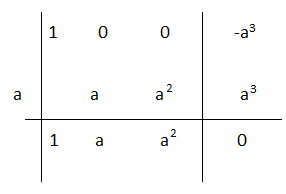
Poichè il resto è 0, il binomio è divisibile per x-a. Calcoliamo il quoziente applicando Ruffini:
Quoziente= x² + ax + a².
Dunque il binomio x³ – a³ può essere scritto come prodotto nel seguente modo:
x³ – a³ = (x-a)( x² + ax + a²)
x³ + a³= (x+a)( x² – ax + a²)