Consideriamo le rette di equazione:
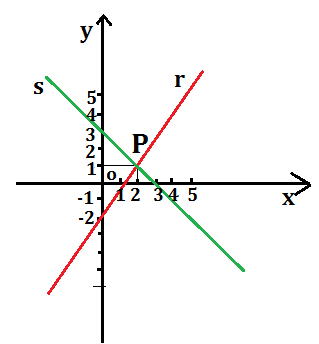
r: y=3\2x-2 e s: y=-x+3
Determiniamo graficamente le coordinate del loro punto d’intersezione. La prima equazione rappresenta la retta r, mentre la seconda la retta s. Queste rette s’incontrano nel punto P che ha l’ascissa +2 e l’ordinata +1, come indicato in figura. Abbiamo cioè P(+2,+1).
Possiamo verificare il risultato nel seguente modo. Poichè il punto P è l’intersezione delle due rette, la sua ordinata è la stessa sia che consideriamo P appartenente ad r sia che lo consideriamo appartenente ad s. Perciò uguagliando i secondi membri delle due equazioni abbiamo:
3\2 x-2= -x+3 da cui ricaviamo facendo il m.c.m.
3 x-4 = -2x+6 ⇒ 5x =+10 ⇒ x=2
Andando a sostituire la x ottenuta in una delle due equazioni delle rette, per comodità si sceglie quella più semplice, e si ottiene l’ordinata del punto d’intersezione quindi:
y=-x+3 ⇒ y=-2+3=+1.
Abbiamo cioè la conferma di quello che già abbiamo individuato graficamente e cioè che il punto d’intersezione tra le due rette P(2,1).
Esercizio n ° 1
Determina graficamente le coordinate del punto di intersezione delle rette
r : y = 2x – 1 s : y = – x + 5
e verifica che il punto trovato appartiene a entrambe.
Si rappresentano le due rette ( è sufficiente determinare le coordinate di due punti), le tabelle dei valori sono:
retta r
| x | -2 | 0 |
| y | -5 | -1 |
retta s
| x | 0 | +3 |
| y | +5 | +2 |
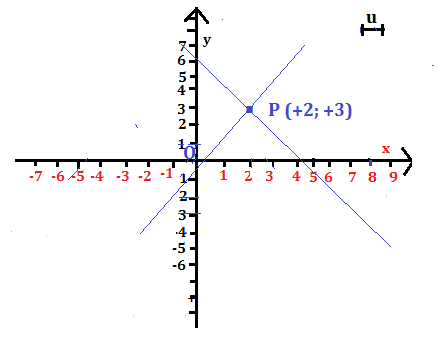
La rappresentazione grafica è:
Dal grafico si ricavano le coordinate del punto P di intersezione: P( +2; +3)
Sostituendo le coordinate di P nell’equazione delle due rette si ottiene:
r: +3 = 2 (+2) -1 +3 = +4 -1 +3 = +3
s: +3 = – (+2) +5 +3 = -2 + 5 +3 = +3
Quindi il punto appartiene a entrambe le rette.
Esercizio n° 2
Con il metodo della risoluzione di un’equazione, determina le coordinate del punto d’intersezione delle rette:
r: y = -x + 2 s: y = +3x – 6
L’ascissa del punto di intersezione P è data dalla risoluzione dell’equazione:
– x +2 = + 3x – 6 si applica la regola del trasporto, scrivendo i termini con la x al 1° membro e i termini noti al 2° membro:
– 3x – x = -6 -2 si riducono i termini simili:
– 4x = -8 si ottiene l’ascissa del punto P:
= + 2
Sostituendo questo valore in una delle equazioni delle rette si ottiene: = -2 + 2 = 0
Quindi P (+2; 0)
Esercizio n° 3
Risolvi il seguente problema
Assumi come unità di misura il cm e rappresenta in un piano cartesiano le rette r ed s di equazione:
r: y = – 2x + 1 s: y = x + 4
Dopo avere indicato con A il loro punto di intersezioni e con B e C i punti in cui le rette incontrano l’asse y, calcola l’area del triangolo ABC.
Svolgimento
Le tabelle dei valori sono:
r: y = – 2x +1
| x | y |
| -2 | +5 |
| 0 | +1 |
s: y = x + 4
| x | y |
| -2 | +2 |
| 0 | +4 |