In un sistema di riferimento cartesiano è possibile determinare la distanza tra due punti. Si possono verificare varie situazioni.
SEGMENTI ORIZZONTALI (con la stessa ordinata)
La distanza tra due punti A e B aventi la stessa ordinata è data dal valore assoluto della differenza tra le ascisse dei due punti.
Si considera il valore assoluto perchè la misura di un segmento non può essere mai negativa.
Se chiamiamo e
le ascisse dei punti abbiamo: AB=|
–
|.
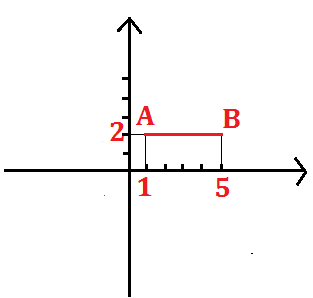
Calcoliamo per esempio la lunghezza del segmento AB i cui estremi hanno coordinate: A(1;2) B(5;2):
AB=| –
|.=| -1-(-5) |=-1 +5=+4.
Si possono anche invertire facendo | –
| e il risultato sarà sempre +4
Ovviamente il valore del segmento, a volte, si può vedere anche ad occhio quando il grafico è disegnato su un foglio a quadretti, allora si potrebbero contare i quadratini per sapere la lunghezza.
SEGMENTI VERTICALI con la stessa ascissa
La distanza tra due punti A e B aventi la stessa ascissa è data dal valore assoluto della differenza fra le ordinate dei due punti.
AB=| –
|.
Si considera il valore assolto perchè un segmento non può essere mai negativo.
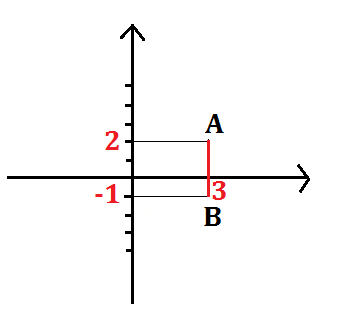
Calcoliamo la lunghezza del segmento AB i cui estremi hanno coordinate A(3;2) e B(3;1)
Sul grafico osserviamo che la lunghezza del segmento AB è 3u.
Otteniamo lo stesso risultato applicando la formula:
AB=| –
|.=| 2-(-1)|=| 2+1|=+3
Se si dovesse fare un segmento verticale su di un foglio a quadretti dove ogni unità è rappresentata da un quadratino, se fossimo in difficoltà potremmo contare semplicemente i quadratini da un estremo all’altro.
SEGMENTI OBLIQUI: DISTANZA TRA DUE PUNTI GENERICI
La misura della distanza tra due punti è uguale alla radice quadrata della somma dei quadrati delle differenze delle ascisse e delle ordinate dei punti.
Siano A e B due punti aventi rispettivamente per coordinate i numeri ,
e
,
; cioè A(
,
) e B(
,
).
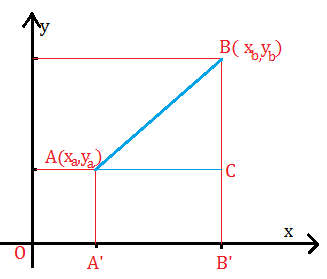
Indichiamo con A’ e B’ le proiezioni di A e B sull’asse x avremo:
OB’=; OA’=
; B’B=
; B’C= ,
allora:
AC= OB’-OA’ =–
CB= B’B – B’C = –
Applicando il teorema di Pitagora al triangolo ABC avremo:
AB=
ESEMPIO
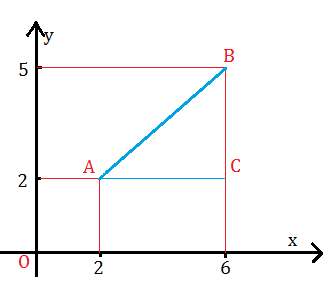
Calcolare la misura della distanza dei punti A(2,2) e B(6,5).
Si ha :
AB=
Programma matematica secondo superiore
Programma di matematica terzo superiore