GLI STRUMENTI DI MISURA
Gli strumenti di misura i dividono in analogici e digitali. Nei primi il valore della misura si legge su una scala graduata, invece negli strumenti digitali il valore della misura appare sul display come una sequenza di cifre.
Inoltre le misure si possono dividere in dirette e indirette. Le prime sono quando la grandezza da misurare è messa a confronto direttamente con la sua unità di misura; le misure indirette sono quelle che si effettuano grazie a calcoli matematici.
Quando si parla di misurare una grandezza bisogna considerare la precisione del valore ottenuto che appunto è dettata dalla precisione dello strumento.
Uno strumento è preciso se , misurando più volte la stessa grandezza, si ottiene sempre lo stesso valore, inoltre le sue misure sono uguali a quelle degli altri strumenti considerati affidabili.
Possiamo quindi dire che la precisione di uno strumento è indice della sua qualità.
PORTATA, CAMPO DI MISURA, SENSIBILITA’ E PRONTEZZA
La portata, detta anche valore di fondo scala è il massimo valore che può essere misurato da uno strumento che rileva la grandezza a partire dal valore zero.
Per esempio se si dice che un righello ha una portata da 50 cm significa che non può misurare grandezze superiori a 50 cm.
Il campo di misura di uno strumento individua l’insieme dei valori che esso è in grado di misurare. Per esempio un termometro clinico ha un campo di misura che va da 35°C a 42°C.
La sensibilità di uno strumento è il più piccolo valore della grandezza che lo strumento può misurare. Per esempio la sensibilità di un righello, che è uno strumento analogico, è di un millimetro e corrisponde alla distanza tra due tacche consecutive. Invece negli strumenti digitali corrisponde al valore della più piccola variazione dell’ultima cifra a destra del display.
Più è piccolo il valore della grandezza che si riesce a distinguere, maggiore è la sensibilità dello strumento La prontezza di uno strumento indica la rapidità con cui risponde a una variazione della quantità da misurare. Per esempio una bilancia da cucina è uno strumento molto pronto visto che il peso di ciò che vogliamo misurare subito ci viene dato a differenza di un termometro clinico che impiega alcuni minuti per indicare la temperatura.
GLI ERRORI CASUALI E SISTEMATICI
Gli errori casuali variano in modo imprevedibile da una misurazione all’altra e possono influenzare il risultato qualche volta per eccesso e qualche volta per difetto.
Essi possono dipendere dall’imprecisione di chi compie la misura, da variazioni imprevedibili della grandezza misurata e dalla variazione delle condizioni in cui avviene l’esperimento. Un errore che avviene di frequente è il non allineare in modo preciso lo zero del righello che risulterà spostato o un po’ a destra o un po’ a sinistra. Poi potrebbe esserci l’errore di parallasse che dipende dalla posizione dei nostri occhi rispetto all’indice dello strumento.
Li errori casuali non possono essere eliminati completamente ma possono essere ridotti ripetendo più volte la stessa misura.
Gli errori sistematici sono quegli errori che avvengono sempre nello stesso senso: o sempre per eccesso o sempre per difetto. Essi sono causati non solo dalla mancata taratura di uno strumento ma possono dipendere anche dal malfunzionamento dello stesso . Per esempio se usiamo un cronometro starato che va avanti, otterremo tutti risultati saranno maggiori di quelli reali.
L’INCERTEZZA DELLE MISURE
E’ impossibile fare una misura esatta: a ogni misura è associata un’incertezza , che può essere più o meno grande.
L’incertezza è sempre presente perchè gli strumenti hanno una sensibilità limitata, quindi esisterà sempre uno strumenti che avrà una sensibilità maggiore è darà un valore più preciso, ma mai certo al cento per cento. E poi abbiamo visto che esistono gli errori.
Quindi per qualsiasi misurazione effettuata al valore ottenuto bisognerà aggiungere un valore che corrisponde all’incertezza quindi:

INCERTEZZA DELLA MISURA SINGOLA
Quando misuriamo con un righello una grandezza, non facciamo più misurazioni, ma una singola. Quindi in questo caso l’incertezza è la sensibilità dello strumento; se per esempio il righello ha una sensibilità di 1 mm e la lunghezza misurata è 10,4 cm allora il risultato lo scriveremo come: L= (10,4 +\- 0,1)cm; si scrive più o meno perchè al risultato della misura va da (10,4 -01) cm a (10,4 +0,1) cm quindi tra 10,3 e 10,5.
Quindi possiamo dire che in generale l’incertezza di una misura singola la possiamo scrivere come:
x= valore misurato +\- sensibilità strumento
IL VALORE MEDIO E L’INCERTEZZA
Se nel misurare qualcosa facciamo più misure, come risultato si sceglierò il valore medio che sarebbe il rapporto tra la somma delle misure e il numero delle misure:

quindi x segnato è il valore medio, invece n sarebbe il numero di misurazioni effettuate.
Facciamo un esempio e consideriamo la misurazione del tempo che ci vuole per un pendolo a compiere sei oscillazioni complete. Si può notare come i valori trovati siano diversi perchè nello svolgere la misura sono stati fatti degli errori casuali.
| MISURA | VALORE(s) |
| 1 | 13,4 |
| 2 | 13,7 |
| 3 | 13,5 |
| 4 | 13,3 |
| 5 | 13,6 |
| 6 | 13,4 |
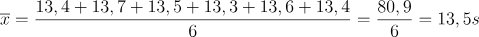
SEMIDISPERSIONE MASSIMA O ERRORE MASSIMO
Si dice semidispersione massima perchè più sono dispersi i dati, cioè quanto più sono diversi tra loro, tanto più la misura è incerta.
Questa semidispersione chiamata anche errore massimo è un modo semplice di stimare l’incertezza dovuta agli errori casuali.
L’err0re massimo è uguale alla differenza tra il valore massimo e il valore minimo diviso due:

Nel caso della tabella precedente l’errore massimo chiamato anche errore assoluto sarà uguale:
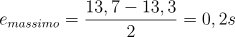
Quindi se dovessimo scrivere quanto tempo impiega il pendolo a compire sei oscillazioni complete scriveremo il valore medio trovato quindi:

Quindi scritta come regola generale avremo:
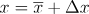
Δx è l’incertezza , invece è il valore medio.
Quindi l’incertezza viene ad essere il più grande tra l’errore massimo e la sensibilità dello strumento..
Nel caso dell’esempio fatto del pendolo abbiano che la sensibilità dello strumento è 0,1 s , mentre l’errore massimo è 0,2 s, quindi l’incertezza è 0,2.
L’incertezza associata a una misura non può essere mai più piccola della sensibilità dello strumento di misura.
INCERTEZZA RELATIVA
Gli errori sistematici possono essere ridotti di molto con un po’ di esperienza e in molti casi in questo modo non incidono sul risultato della misura. Tutto ciò può portare ad ottenere delle misure con una buona accuratezza.
Appunto una misura si dice accurata quanto più il valore medio delle misure eseguite si avvicina al valore esatto della grandezza.
Oltre all’accuratezza si può citare anche la precisione di una misura; una misura è tanto più precisa quanto più i singoli valori misurati si concentrano intorno al valore medio delle misure eseguite. Ovviamente una misura molto precisa è difficile da ottenere, perchè ridurre l’incertezza dovuta agli errori casuali non è semplice.
Per indicare quanto una misura è precisa si usa l’incertezza relativa che si indica con e corrisponde al rapporto tra l’incertezza e il valore più attendibile quindi:
Per esempio l’incertezza relativa della misura
Importante notare che l’errore relativo o incertezza relativa è adimensionale perchè dato dal rapporto di due grandezze uguali.
L’incertezza relativa può anche essere espressa in percentuale:
Nel caso dell’esempio precedente l’incertezza percentuale è= 0,007 • 100 = 0,7%
L’incertezza relativa è anche utile per confrontare delle grandezze. Per esempio :
1° grandezza l= (4,26 ± 0,03) cm
2° grandezza L= (120,4± 0,1) m
La seconda grandezza ha l’errore assoluto maggiore però se andiamo a calcolare l’incertezza relativa vediamo che per la prima è 0,007 per la seconda 0,0008 quindi più piccola nonostante il suo errore assoluto fosse più grande.
L’ERRORE STATISTICO O INCERTEZZA STATISTICA
Quando abbiamo un numero di misurazioni abbastanza elevato a disposizione possiamo dare una valutazione dell’incertezza abbastanza accurato rispetto alla semidispersione massima.
Supponiamo di aver eseguito n misure di una grandezza, come ben sappiamo il valore più attendibile è la media dei valori trovati.
Quando il numero n, quindi le misurazioni sono un numero maggiore di 10, si assume come incertezza lo scarto quadratico medio.
Esso si indica con σ (sigma) ed è:
La stima della misura si scriverà:
Visto che l’errore assoluto prende in considerazione solo il valore massimo e il valore minimo è meno attendibile dello scarto quadratico medio che considera tutte le misure effettuate.
L’incertezza da associare alla misura è il massimo tra la sensibilità dello strumento e lo scarto quadratico medio.
In generale lo scarto quadratico medio è minore dell’errore assoluto.
Se dovessimo rappresentare i valori delle varie misure su un istogramma , la sua forma tende ad essere quella di una campana chiamata curva di Gauss.
INCERTEZZA IN UN AMISURA INDIRETTA
Una misura indiretta ottenuta mediante uno misurazione affetta da incertezze ha sempre un’incertezza maggiore o uguale a quella della misura più incerta.
Vediamo quali sono le regole:
- L’incertezza della somma di due o più misure è la somma delle incertezze delle misure , anche la differenza di due o più misure è la somma delle incertezze delle misure
Δ(a+b) = Δa + Δb Per esempio (1,27 ± 0,02)kg e (2,18 ± 0,03)kg il valore totale sarà 1,27+2,18 = 3,45 kg e l’incertezza è la somma delle incertezze 0,02 + 0,03 = 0,05 kg. Lo stesso vale per la differenza.
- L’incertezza del prodotto di una misura per una costante è il prodotto dell’incertezza della misura per la costante.
- L’incertezza relativa del prodotto di due o più misure è la somma delle incertezze relative delle misure:
- L’incertezza relativa al quoziente di due o più misure è la somma delle incertezze relative delle misure:
PROGRAMMA DI FISICA SUPERIORI