La regola di Ruffini ci permette senza eseguire la divisione di calcolare il quoziente e il resto della divisione di un polinomio per il binomio x-a, dove a è un numero reale qualunque.
Per esempio per eseguire la divisione (3x² – 10x – 9) : (x – 4)

Quindi il quoziente dovrà essere di grado 1 perchè un grado in meno rispetto al dividendo originario, infatti sarà 3x +2; il resto sarà -1.
Per verificare come per la divisione tra due polinomi si farà A= quoziente per divisore più il resto, quindi: (3x + 2)(x-4) + (-1)
Se il divisore è nella forma x+a si può sempre applicare Ruffini perchè si considera x+a = x- (-a).
Ricordiamo che se il dividendo non è un polinomio completo si dovranno mettere nella prima riga dei coefficienti 0 al posto dei termini mancanti. Per esempio: -5x² +8x -10 dobbiamo dividerla per x+3.
Prima di tutto x+3= x – (-3). Poi poichè manca il termine elevato alla terza al suo posto verrà messo lo 0.
+ 0 -5x² +8x -10 : x-(-3)
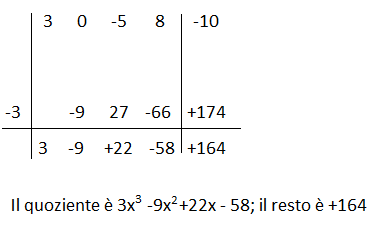
Se sostituendo il termine noto del divisore con il segno cambiato al polinomio, dividendo, si ottiene zero allora quel polinomio sarà divisibile per quel binomio.
Per esempio x³ + x² -9x – 9 vogliamo sapere se è divisibile per x-3 allora effettuiamo la sostituzione.
3³ + 3² -9·3 – 9 = 27 + 9 – 27 – 9 = 0 Il risultato è zero quindi il polinomio è divisibile per x-3.